Search any question & find its solution
Question:
Answered & Verified by Expert
A square loop of length $L$ is placed with its edges parallel to the $X Y$-axes. The loop is carrying the current $I$. If the magnetic field in the region varies as $\mathbf{B}=B_0\left(1+\frac{X y}{L^2}\right) \hat{\mathbf{k}}$, then the magnitude of the force on the loop will be
Options:
Solution:
2095 Upvotes
Verified Answer
The correct answer is:
$1 5IB0l L$
We take one vertex of square loop at origin,
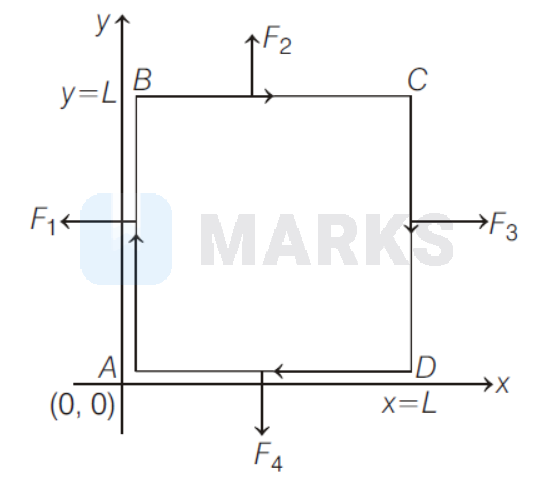
for wire $A B$, magnetic field $A B=B_0(1+0)=B_0$.
$$
\therefore \quad n=0
$$
For wire $C D$, magnetic field $=B_0\left(1+\frac{y}{L}\right)$,
$$
\therefore
$$
$$
x=L
$$
For wire $B C$, magnetic field $=B_0\left(1+\frac{\chi}{L}\right)$,
$$
\therefore \quad y=L
$$
and for wire $A D$, magnetic field $=B_0$
$$
\therefore \quad y=0
$$
Now me calculate forces
$$
F_1, F_2, F_3 \text { and } F_4 \text {, }
$$
$$
\begin{aligned}
F_1 & =\int_0^L I B_0 \mathrm{dy}=I B_0 L \\
F_2 & =\int_0^L I B_0\left(1+\frac{x}{L}\right) d x \\
& =\frac{3}{2} I B_0 L \\
F_3 & =\int_0^I I B_0\left(1+\frac{y}{L}\right) d x \\
& =\frac{3}{2} I B_0 L \\
F_4 & =\int_0^L I B_0 d x=I B_0 L
\end{aligned}
$$

for wire $A B$, magnetic field $A B=B_0(1+0)=B_0$.
$$
\therefore \quad n=0
$$
For wire $C D$, magnetic field $=B_0\left(1+\frac{y}{L}\right)$,
$$
\therefore
$$
$$
x=L
$$
For wire $B C$, magnetic field $=B_0\left(1+\frac{\chi}{L}\right)$,
$$
\therefore \quad y=L
$$
and for wire $A D$, magnetic field $=B_0$
$$
\therefore \quad y=0
$$
Now me calculate forces
$$
F_1, F_2, F_3 \text { and } F_4 \text {, }
$$
$$
\begin{aligned}
F_1 & =\int_0^L I B_0 \mathrm{dy}=I B_0 L \\
F_2 & =\int_0^L I B_0\left(1+\frac{x}{L}\right) d x \\
& =\frac{3}{2} I B_0 L \\
F_3 & =\int_0^I I B_0\left(1+\frac{y}{L}\right) d x \\
& =\frac{3}{2} I B_0 L \\
F_4 & =\int_0^L I B_0 d x=I B_0 L
\end{aligned}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.