Search any question & find its solution
Question:
Answered & Verified by Expert
A square of side a lies above the $x$-axis and has one vertex at the origin. The side passing through the origin makes an angle $\alpha\left(0 < \alpha < \frac{\pi}{4}\right)$ with the positive direction of $\mathrm{x}$-axis. The equation of its diagonal not passing through the origin is
Options:
Solution:
2293 Upvotes
Verified Answer
The correct answer is:
$y(\cos \alpha+\sin \alpha)+x(\cos \alpha-\sin \alpha)=a$
$y(\cos \alpha+\sin \alpha)+x(\cos \alpha-\sin \alpha)=a$
Co-ordinates of $\mathrm{A}=(a \cos \alpha, a \sin \alpha)$
Equation of $\mathrm{OB}, \mathrm{y}=\tan \left(\frac{\pi}{4}+\alpha\right) \mathrm{x}$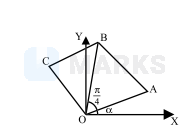
$\mathrm{CA} \perp \mathrm{r}$ to OB $\quad \therefore$ slope of $\mathrm{CA}=-\cot \left(\frac{\pi}{4}+2\right)$
Equation of $\mathrm{CA} \mathrm{y}-\mathrm{a} \sin \alpha=-\cot \left(\frac{\pi}{4}+2\right)(\mathrm{x}-\mathrm{a} \cos \alpha)$
$\mathrm{y}(\sin \alpha+\cos \alpha)+\mathrm{x}(\cos \alpha-\sin \alpha)=\mathrm{a}$
Equation of $\mathrm{OB}, \mathrm{y}=\tan \left(\frac{\pi}{4}+\alpha\right) \mathrm{x}$

$\mathrm{CA} \perp \mathrm{r}$ to OB $\quad \therefore$ slope of $\mathrm{CA}=-\cot \left(\frac{\pi}{4}+2\right)$
Equation of $\mathrm{CA} \mathrm{y}-\mathrm{a} \sin \alpha=-\cot \left(\frac{\pi}{4}+2\right)(\mathrm{x}-\mathrm{a} \cos \alpha)$
$\mathrm{y}(\sin \alpha+\cos \alpha)+\mathrm{x}(\cos \alpha-\sin \alpha)=\mathrm{a}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.