Search any question & find its solution
Question:
Answered & Verified by Expert
A straight conductor carrying current $i$ splits into two parts as shown in the figure. The radius of the circular loop is $R$. The total magnetic field at the centre $P$ at the loop is
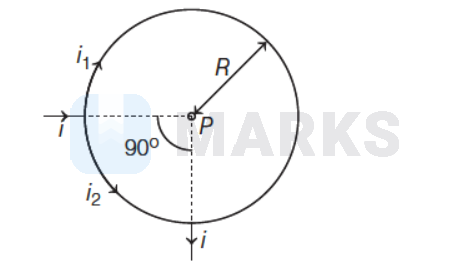
Options:

Solution:
2135 Upvotes
Verified Answer
The correct answer is:
Zero
The magnetic field at the centre of an arc subtended at an angle $\theta$ is given by
$\mathrm{B}=\frac{\mu_0 \mathrm{i}}{2 \mathrm{R}} \times \frac{\theta}{2 \pi}$
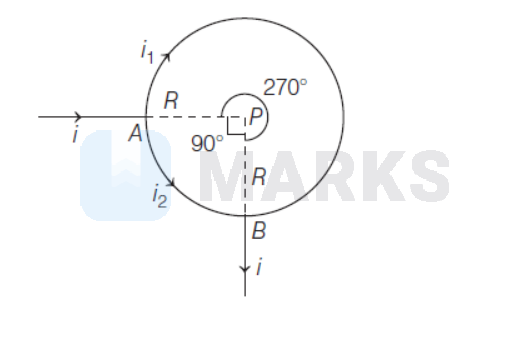
Then, the magnetic field due to larger arc $A B$ is
$\mathrm{B}_1=\frac{\mu_0 \mathrm{i}_1}{2 \mathrm{R}} \times \frac{270}{2 \pi}$
which acts in inward direction according to right hand thumb rule.
And magnetic field due to smaller arc $A B$ is
$\mathrm{B}_2=\frac{\mu_0 \mathrm{i}_2}{2 \mathrm{R}} \times \frac{90}{2 \pi}$
which acts in outward direction.
The resultant magnetic field
$\begin{aligned}
& \mathrm{B}_{\mathrm{R}}=\mathrm{B}_1+\mathrm{B}_2 \\
& =-\frac{\mu_0 \mathrm{i}_1 \times 270}{4 \pi \mathrm{R}}+\frac{\mu_0 \mathrm{i}_2 \times 90}{4 \pi \mathrm{R}} \text { [From Eq. (i) and (ii)] }
\end{aligned}$
which acts in inward direction as $\mathrm{B}_1>\mathrm{B}_2$.
Two arcs can also be seen as the two resistances in parallel combination.
So, the potential across them will be same i.e.
$\begin{aligned}
\mathrm{V}_1 & =\mathrm{V}_2 \\
\mathrm{i}_1 \mathrm{R}_1 & =\mathrm{i}_2 \mathrm{R}_2
\end{aligned}$
where, $\mathrm{R}_1$ and $\mathrm{R}_2=$ Resistance of respective segments
The wire is uniform so
$\begin{aligned}
& \frac{\mathrm{R}_1}{\mathrm{R}_2}=\frac{\mathrm{L}_1}{\mathrm{~L}_2}=\frac{\mathrm{R} \times 270}{\mathrm{R} \times 90} [\because \text { length of arc }=\text { radius } \times \\
& \text { angle] }
\end{aligned}$
From Eq. (iv), we get
$\Rightarrow \frac{\mathrm{i}_1}{\mathrm{i}_2}=\frac{\mathrm{R}_2}{\mathrm{R}_1}=\frac{90}{270}=\frac{1}{3}$
or $3 i_1=i_2$
From Eq. (iii) and (v), we get
$\begin{aligned}
\mathrm{B}_{\mathrm{R}} & =\frac{\mu_0}{4 \pi \mathrm{R}}\left(-270 \mathrm{i}_1+90 \mathrm{i}_2\right) \\
& =\frac{\mu_0}{4 \pi R}\left[-270 \mathrm{i}_1+90\left(3 \mathrm{i}_1\right)\right] \\
& =\frac{\mu_0}{4 \pi \mathrm{R}}\left(-270 \mathrm{i}_1+270 \mathrm{i}_1\right)=0
\end{aligned}$
$\mathrm{B}=\frac{\mu_0 \mathrm{i}}{2 \mathrm{R}} \times \frac{\theta}{2 \pi}$

Then, the magnetic field due to larger arc $A B$ is
$\mathrm{B}_1=\frac{\mu_0 \mathrm{i}_1}{2 \mathrm{R}} \times \frac{270}{2 \pi}$
which acts in inward direction according to right hand thumb rule.
And magnetic field due to smaller arc $A B$ is
$\mathrm{B}_2=\frac{\mu_0 \mathrm{i}_2}{2 \mathrm{R}} \times \frac{90}{2 \pi}$
which acts in outward direction.
The resultant magnetic field
$\begin{aligned}
& \mathrm{B}_{\mathrm{R}}=\mathrm{B}_1+\mathrm{B}_2 \\
& =-\frac{\mu_0 \mathrm{i}_1 \times 270}{4 \pi \mathrm{R}}+\frac{\mu_0 \mathrm{i}_2 \times 90}{4 \pi \mathrm{R}} \text { [From Eq. (i) and (ii)] }
\end{aligned}$
which acts in inward direction as $\mathrm{B}_1>\mathrm{B}_2$.
Two arcs can also be seen as the two resistances in parallel combination.
So, the potential across them will be same i.e.
$\begin{aligned}
\mathrm{V}_1 & =\mathrm{V}_2 \\
\mathrm{i}_1 \mathrm{R}_1 & =\mathrm{i}_2 \mathrm{R}_2
\end{aligned}$
where, $\mathrm{R}_1$ and $\mathrm{R}_2=$ Resistance of respective segments
The wire is uniform so
$\begin{aligned}
& \frac{\mathrm{R}_1}{\mathrm{R}_2}=\frac{\mathrm{L}_1}{\mathrm{~L}_2}=\frac{\mathrm{R} \times 270}{\mathrm{R} \times 90} [\because \text { length of arc }=\text { radius } \times \\
& \text { angle] }
\end{aligned}$
From Eq. (iv), we get
$\Rightarrow \frac{\mathrm{i}_1}{\mathrm{i}_2}=\frac{\mathrm{R}_2}{\mathrm{R}_1}=\frac{90}{270}=\frac{1}{3}$
or $3 i_1=i_2$
From Eq. (iii) and (v), we get
$\begin{aligned}
\mathrm{B}_{\mathrm{R}} & =\frac{\mu_0}{4 \pi \mathrm{R}}\left(-270 \mathrm{i}_1+90 \mathrm{i}_2\right) \\
& =\frac{\mu_0}{4 \pi R}\left[-270 \mathrm{i}_1+90\left(3 \mathrm{i}_1\right)\right] \\
& =\frac{\mu_0}{4 \pi \mathrm{R}}\left(-270 \mathrm{i}_1+270 \mathrm{i}_1\right)=0
\end{aligned}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.