Search any question & find its solution
Question:
Answered & Verified by Expert
A straight line $L$ through the point $(3,-2)$ is inclined at an angle $60^{\circ}$ to the line $\sqrt{3} x+y=1$. If $L$ also intersects the $X$-axis, then the equation of $L$ is
Options:
Solution:
1531 Upvotes
Verified Answer
The correct answer is:
$y-\sqrt{3} x+2+3 \sqrt{3}=0$
$y-\sqrt{3} x+2+3 \sqrt{3}=0$
A straight line passing through $P$ and making an angle of $\alpha=60^{\circ}$, is given by $\frac{y-y_1}{x-x_1}=\tan (\theta \pm \alpha)$
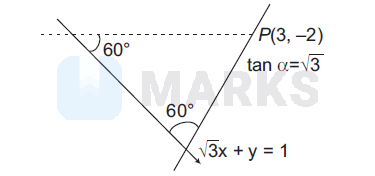
where, $\quad \sqrt{3} x+y=1$
$$
\Rightarrow \quad y=-\sqrt{3} x+1
$$
Then, $\quad \tan \theta=-\sqrt{3}$
$$
\begin{array}{ll}
\Rightarrow & \frac{y+2}{x-3}=\frac{\tan \theta \pm \tan \alpha}{1 \mp \tan \theta \tan \alpha} \\
\Rightarrow & \frac{y+2}{x-3}=\frac{-\sqrt{3}+\sqrt{3}}{1-(-\sqrt{3})(\sqrt{3})} \\
\text { and } & \frac{y+2}{x-3}=\frac{-\sqrt{3}-\sqrt{3}}{1+(-\sqrt{3})(\sqrt{3})}
\end{array}
$$
$$
\begin{array}{ll}
\Rightarrow & y+2=0 \\
\text { and } & \frac{y+2}{x-3}=\frac{-2 \sqrt{3}}{1-3}=\sqrt{3} \\
\Rightarrow & y+2=\sqrt{3} x-3 \sqrt{3}
\end{array}
$$
Neglecting, $y+2=0$ as it does not intersect $Y$-axis.
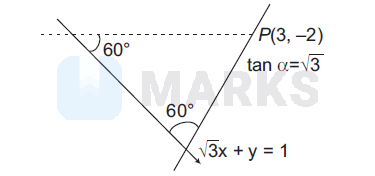
where, $\quad \sqrt{3} x+y=1$
$$
\Rightarrow \quad y=-\sqrt{3} x+1
$$
Then, $\quad \tan \theta=-\sqrt{3}$
$$
\begin{array}{ll}
\Rightarrow & \frac{y+2}{x-3}=\frac{\tan \theta \pm \tan \alpha}{1 \mp \tan \theta \tan \alpha} \\
\Rightarrow & \frac{y+2}{x-3}=\frac{-\sqrt{3}+\sqrt{3}}{1-(-\sqrt{3})(\sqrt{3})} \\
\text { and } & \frac{y+2}{x-3}=\frac{-\sqrt{3}-\sqrt{3}}{1+(-\sqrt{3})(\sqrt{3})}
\end{array}
$$
$$
\begin{array}{ll}
\Rightarrow & y+2=0 \\
\text { and } & \frac{y+2}{x-3}=\frac{-2 \sqrt{3}}{1-3}=\sqrt{3} \\
\Rightarrow & y+2=\sqrt{3} x-3 \sqrt{3}
\end{array}
$$
Neglecting, $y+2=0$ as it does not intersect $Y$-axis.
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.