Search any question & find its solution
Question:
Answered & Verified by Expert
A system containing masses and pulleys connected on an inclined plane is shown in the figure. If the system is in equilibrium then the value of \(m\) is
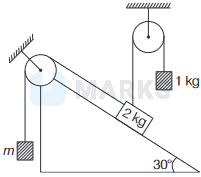
Options:

Solution:
1831 Upvotes
Verified Answer
The correct answer is:
\(0.5 \mathrm{~kg}\)
According to the question, the complete situation is shown in the following figure,
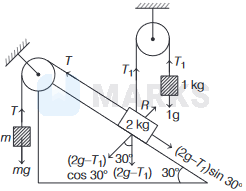
Since, system is in equilibrium, hence
\(\begin{aligned}
T & =m g \quad \ldots (i) \\
T & =\left(2 g-T_1\right) \sin 30^{\circ} \quad \ldots (ii) \\
T_1 & =1 g \quad \ldots (iii)
\end{aligned}\)
\(\therefore\) From Eqs. (ii) and (iii), we get
\(\begin{aligned}
& T=(2 g-\mathbf{l} g) \sin 30^{\circ}=g \sin 30^{\circ} \\
& T=\frac{g}{2} \quad \ldots (iv)
\end{aligned}\)
\(\therefore\) From Eqs. (i) and (iv), we get,
\(\begin{aligned}
m g & =\frac{g}{2} \\
\Rightarrow \quad m & =0.5 \mathrm{~kg}
\end{aligned}\)

Since, system is in equilibrium, hence
\(\begin{aligned}
T & =m g \quad \ldots (i) \\
T & =\left(2 g-T_1\right) \sin 30^{\circ} \quad \ldots (ii) \\
T_1 & =1 g \quad \ldots (iii)
\end{aligned}\)
\(\therefore\) From Eqs. (ii) and (iii), we get
\(\begin{aligned}
& T=(2 g-\mathbf{l} g) \sin 30^{\circ}=g \sin 30^{\circ} \\
& T=\frac{g}{2} \quad \ldots (iv)
\end{aligned}\)
\(\therefore\) From Eqs. (i) and (iv), we get,
\(\begin{aligned}
m g & =\frac{g}{2} \\
\Rightarrow \quad m & =0.5 \mathrm{~kg}
\end{aligned}\)
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.