Search any question & find its solution
Question:
Answered & Verified by Expert
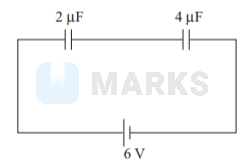
A system of \( 2 \) capacitors of capacitance \( 2 \mu \mathrm{F} \) and \( 4 \mu \mathrm{F} \) is connected in series across a potential
difference of \( 6 \mathrm{~V} \). The electric charge and energy stored in the system are
Options:
difference of \( 6 \mathrm{~V} \). The electric charge and energy stored in the system are
Solution:
2207 Upvotes
Verified Answer
The correct answer is:
\( 8 \mu \mathrm{C} \) and \( 24 \mu \mathrm{J} \)
The effective capacitance of system of two given capacitors is
\[
\begin{array}{l}
=\frac{1}{2 \mu F}+\frac{1}{4 \mu F}=\frac{(2+1)}{4 \mu F}=\frac{3}{4} \\
\Rightarrow C=\frac{4}{3} \mu F
\end{array}
\]
Now, using \( Q=C V \)
\[
Q=\frac{4}{3} \times 10^{-6} \mathrm{~F} \times 6 \mathrm{~V}=8 \times 10^{-6} \mathrm{C}
\]
Therefore, electric charge \( =8 \mu \mathrm{C} \)
Now, energy stored \( =\frac{1}{2} C V^{2}=\frac{1}{2} \times \frac{4}{3} \times 10^{-6} \times 6 \times 6 \)
\( =2 \times 10^{-6} \times 2 \times 6=24 \times 10^{-6} \mathrm{~J} \)
Therefore, energy stored \( =24 \mu \mathrm{J} \)
\[
\begin{array}{l}
=\frac{1}{2 \mu F}+\frac{1}{4 \mu F}=\frac{(2+1)}{4 \mu F}=\frac{3}{4} \\
\Rightarrow C=\frac{4}{3} \mu F
\end{array}
\]
Now, using \( Q=C V \)
\[
Q=\frac{4}{3} \times 10^{-6} \mathrm{~F} \times 6 \mathrm{~V}=8 \times 10^{-6} \mathrm{C}
\]

Therefore, electric charge \( =8 \mu \mathrm{C} \)
Now, energy stored \( =\frac{1}{2} C V^{2}=\frac{1}{2} \times \frac{4}{3} \times 10^{-6} \times 6 \times 6 \)
\( =2 \times 10^{-6} \times 2 \times 6=24 \times 10^{-6} \mathrm{~J} \)
Therefore, energy stored \( =24 \mu \mathrm{J} \)
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.