Search any question & find its solution
Question:
Answered & Verified by Expert
A tennis ball (treated as hollow spherical shell) starting from $\mathrm{O}$ rolls down a hill. At point $\mathrm{A}$ the ball becomes air borne leaving at an angle of $30^{\circ}$ with the horizontal. The ball strikes the ground at $\mathrm{B}$. What is the value of the distance $\mathrm{AB}$ ?
(Moment of inertia of a spherical shell of mass $m$ and radius $R$ about its diameter $=\frac{2}{3} m R^2$ )
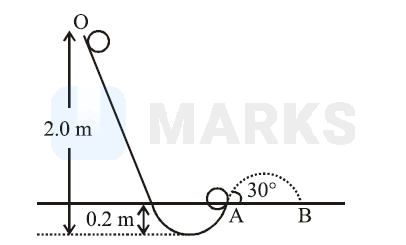
Options:
(Moment of inertia of a spherical shell of mass $m$ and radius $R$ about its diameter $=\frac{2}{3} m R^2$ )

Solution:
2746 Upvotes
Verified Answer
The correct answer is:
$2.08 \mathrm{~m}$
$2.08 \mathrm{~m}$
Velocity of the tennis ball on the surface of the earth or ground
$$
\begin{aligned}
& \mathrm{v}=\sqrt{\frac{2 \mathrm{gh}}{1+\frac{\mathrm{k}^2}{\mathrm{R}^2}}}(\text { where } \mathrm{k}=\text { radius of gyration } \\
& \text { of spherical shell } \left.=\sqrt{\frac{2}{3}} \mathrm{R}\right) \\
& \text { Horizontal range } \mathrm{AB}=\frac{\mathrm{v}^2 \sin 2 \theta}{\mathrm{g}} \\
& =\frac{\left.\sqrt{\frac{2 \mathrm{gh}}{1+\mathrm{k}^2 / \mathrm{R}^2}}\right)^2 \sin \left(2 \times 30^{\circ}\right)}{\mathrm{g}}
\end{aligned}
$$
$$
\begin{aligned}
& \mathrm{v}=\sqrt{\frac{2 \mathrm{gh}}{1+\frac{\mathrm{k}^2}{\mathrm{R}^2}}}(\text { where } \mathrm{k}=\text { radius of gyration } \\
& \text { of spherical shell } \left.=\sqrt{\frac{2}{3}} \mathrm{R}\right) \\
& \text { Horizontal range } \mathrm{AB}=\frac{\mathrm{v}^2 \sin 2 \theta}{\mathrm{g}} \\
& =\frac{\left.\sqrt{\frac{2 \mathrm{gh}}{1+\mathrm{k}^2 / \mathrm{R}^2}}\right)^2 \sin \left(2 \times 30^{\circ}\right)}{\mathrm{g}}
\end{aligned}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.