Search any question & find its solution
Question:
Answered & Verified by Expert
A thin converging lens of focal length $f=25 \mathrm{~cm}$ forms the image of an object on a screen placed at a distance of $75 \mathrm{~cm}$ from the lens. The screen is moved closer to the lens by a distance of $25 \mathrm{~cm}$. The distance through which the object has to be shifted, so that its image on the screen in sharp again is
Options:
Solution:
2427 Upvotes
Verified Answer
The correct answer is:
$12.5 \mathrm{~cm}$
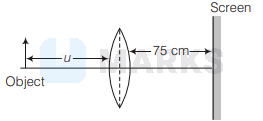
According to the first condition,
$$
\begin{aligned}
f & =25 \mathrm{~cm}, v=75 \mathrm{~cm} \\
u & =? \\
\frac{1}{f} & =\frac{1}{v}-\frac{1}{u} \\
\frac{1}{25} & =\frac{1}{75}-\frac{1}{u} \\
\frac{1}{u} & =\frac{1}{75}-\frac{1}{25} \\
\frac{1}{u} & =\frac{1-3}{75} \\
u & =-\frac{75}{2}=-37.5 \mathrm{~cm}
\end{aligned}
$$
According to the second condition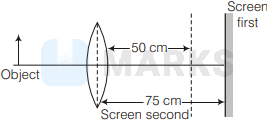
$$
\begin{aligned}
v_1=50 \mathrm{~cm}, f & =25 \mathrm{~cm}, u_1=? \\
\frac{1}{f} & =\frac{1}{v_1}-\frac{1}{u_1} \\
\frac{1}{25} & =\frac{1}{50}-\frac{1}{u_1} \\
\frac{1}{u_1} & =\frac{1}{50}-\frac{1}{25} \\
\Rightarrow \quad \frac{1}{u_1} & =\frac{1-2}{50} \\
\Rightarrow \quad u_1 & =-50 \mathrm{~cm}
\end{aligned}
$$
So, the screen is sharp again is
$$
\begin{aligned}
\Delta u & =u_1-u \\
& =50-37.5 \\
& =12.5 \mathrm{~cm}
\end{aligned}
$$

$$
\begin{aligned}
f & =25 \mathrm{~cm}, v=75 \mathrm{~cm} \\
u & =? \\
\frac{1}{f} & =\frac{1}{v}-\frac{1}{u} \\
\frac{1}{25} & =\frac{1}{75}-\frac{1}{u} \\
\frac{1}{u} & =\frac{1}{75}-\frac{1}{25} \\
\frac{1}{u} & =\frac{1-3}{75} \\
u & =-\frac{75}{2}=-37.5 \mathrm{~cm}
\end{aligned}
$$
According to the second condition

$$
\begin{aligned}
v_1=50 \mathrm{~cm}, f & =25 \mathrm{~cm}, u_1=? \\
\frac{1}{f} & =\frac{1}{v_1}-\frac{1}{u_1} \\
\frac{1}{25} & =\frac{1}{50}-\frac{1}{u_1} \\
\frac{1}{u_1} & =\frac{1}{50}-\frac{1}{25} \\
\Rightarrow \quad \frac{1}{u_1} & =\frac{1-2}{50} \\
\Rightarrow \quad u_1 & =-50 \mathrm{~cm}
\end{aligned}
$$
So, the screen is sharp again is
$$
\begin{aligned}
\Delta u & =u_1-u \\
& =50-37.5 \\
& =12.5 \mathrm{~cm}
\end{aligned}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.