Search any question & find its solution
Question:
Answered & Verified by Expert
A thin flexible wire of length $L$ is connected to two adjacent fixed points and carries a current $I$ in the clockwise direction as shown. When the system is put in uniform magnetic field of strength $B$ going into the plane of the paper, the wire take the shape of a circle. The tension in the wire, after acquiring the circular shape is
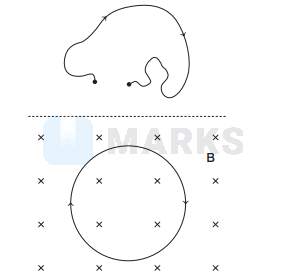
Options:

Solution:
1317 Upvotes
Verified Answer
The correct answer is:
$\frac{I B L}{2 \pi}$
Given that, the length of wire $=L$
Current passing through ring $=I$
Let $R$ be the radius of ring.
Then, $2 \pi R=L$
$$
R=\frac{L}{2 \pi}...(i)
$$
Consider an element of ring $A B$ which subtends an angle $\Delta \theta$ at the centre $O$,
such that, $A B=\Delta l=R \Delta \theta$...(ii)
If $T$ be the tension at point $P$ as shown in figure.
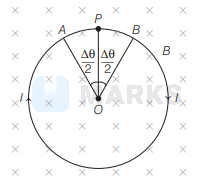
We know that, force acting on element $A B$ in uniform magnetic field,
$$
F=I B \Delta l
$$
... (iii) (radially outward)
By resolving tension into sine and cosine components $T \cos \frac{\Delta \theta}{2}$ is acting equal and opposite.
So, it is cancelled.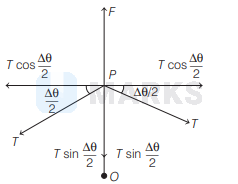
But sum of sine component is equal and opposite to $F$.
$\therefore$ At equilibrium, we get
$$
2 T \sin \frac{\Delta \theta}{2}=F
$$
As $\frac{\Delta \theta}{2}$ is very small angle, so, $\sin \frac{\Delta \theta}{2}=\frac{\Delta \theta}{2}$
By substituting the values, we get
$$
\begin{aligned}
2 T \frac{\Delta \theta}{2} & =I B \Delta l \Rightarrow T \Delta \theta=I B R \Delta \theta \\
T & =I B R...(i)
\end{aligned}
$$
Using Eqs. (i) and (iv), we get
$$
T=I B L / 2 \pi
$$
Current passing through ring $=I$
Let $R$ be the radius of ring.
Then, $2 \pi R=L$
$$
R=\frac{L}{2 \pi}...(i)
$$
Consider an element of ring $A B$ which subtends an angle $\Delta \theta$ at the centre $O$,
such that, $A B=\Delta l=R \Delta \theta$...(ii)
If $T$ be the tension at point $P$ as shown in figure.

We know that, force acting on element $A B$ in uniform magnetic field,
$$
F=I B \Delta l
$$
... (iii) (radially outward)
By resolving tension into sine and cosine components $T \cos \frac{\Delta \theta}{2}$ is acting equal and opposite.
So, it is cancelled.

But sum of sine component is equal and opposite to $F$.
$\therefore$ At equilibrium, we get
$$
2 T \sin \frac{\Delta \theta}{2}=F
$$
As $\frac{\Delta \theta}{2}$ is very small angle, so, $\sin \frac{\Delta \theta}{2}=\frac{\Delta \theta}{2}$
By substituting the values, we get
$$
\begin{aligned}
2 T \frac{\Delta \theta}{2} & =I B \Delta l \Rightarrow T \Delta \theta=I B R \Delta \theta \\
T & =I B R...(i)
\end{aligned}
$$
Using Eqs. (i) and (iv), we get
$$
T=I B L / 2 \pi
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.