Search any question & find its solution
Question:
Answered & Verified by Expert
A thin rod of length 41 and mass $4 \mathrm{~m}$ is bent at the points as shown in figure. What is the moment of inertia of the rod about the axis passes through point $\mathrm{O}$ and perpendicular to the plane of paper?
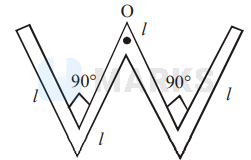
Options:

Solution:
2569 Upvotes
Verified Answer
The correct answer is:
$\frac{10 \mathrm{M} l^{2}}{3}$
Total moment of inertia
$$
=\mathrm{I}_{1}+\mathrm{I}_{2}+\mathrm{I}_{3}+\mathrm{I}_{4}=2 \mathrm{I}_{1}+2 \mathrm{I}_{2}
$$
$$
\begin{array}{l}
=2\left(l_{1}+l_{2}\right)\left\lceil I_{3}=I_{1}, I_{1}=I_{4}\right] \\
\text { Now, } I_{2}=I_{3}=\frac{M I^{2}}{3}
\end{array}
$$
Using parallel axes theorem, we have
$$
\begin{array}{l}
\mathrm{I}=\mathrm{I}_{\mathrm{CM}}+\mathrm{Mx}^{2} \text { and } \mathrm{x}=\sqrt{l^{2}+\frac{l^{2}}{4}} \\
\mathrm{I}_{1}=\mathrm{I}_{4}=\frac{\mathrm{M} l^{2}}{12}+\mathrm{M}\left[\sqrt{l^{2}+\left(\frac{l}{2}\right)^{2}}\right]^{2}
\end{array}
$$
Putting all values we get Moment of inertia, $\mathrm{I}=10\left(\frac{\mathrm{Ml}^{2}}{3}\right)$
$$
=\mathrm{I}_{1}+\mathrm{I}_{2}+\mathrm{I}_{3}+\mathrm{I}_{4}=2 \mathrm{I}_{1}+2 \mathrm{I}_{2}
$$
$$
\begin{array}{l}
=2\left(l_{1}+l_{2}\right)\left\lceil I_{3}=I_{1}, I_{1}=I_{4}\right] \\
\text { Now, } I_{2}=I_{3}=\frac{M I^{2}}{3}
\end{array}
$$
Using parallel axes theorem, we have
$$
\begin{array}{l}
\mathrm{I}=\mathrm{I}_{\mathrm{CM}}+\mathrm{Mx}^{2} \text { and } \mathrm{x}=\sqrt{l^{2}+\frac{l^{2}}{4}} \\
\mathrm{I}_{1}=\mathrm{I}_{4}=\frac{\mathrm{M} l^{2}}{12}+\mathrm{M}\left[\sqrt{l^{2}+\left(\frac{l}{2}\right)^{2}}\right]^{2}
\end{array}
$$
Putting all values we get Moment of inertia, $\mathrm{I}=10\left(\frac{\mathrm{Ml}^{2}}{3}\right)$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.