Search any question & find its solution
Question:
Answered & Verified by Expert
A toroid has a core of inner radius $r_1$ and outer radius $r_2$, around which $N$ turns of wire are wound. If the current in the wire is $I$ then the magnetic field inside the toroid is ( $\mu_0=$ permeability of free space)
Options:
Solution:
2204 Upvotes
Verified Answer
The correct answer is:
$\frac{\mu_0 N I}{\pi\left(r_1+r_2\right)}$
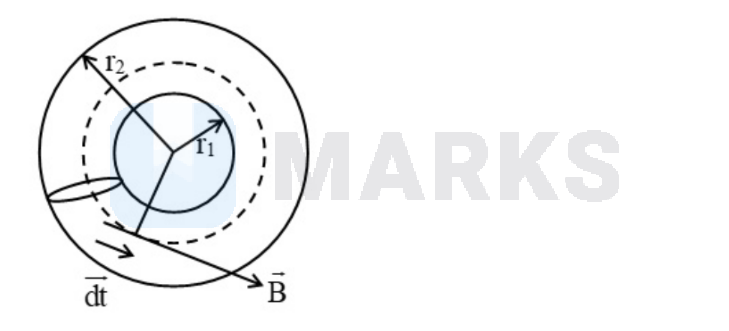
Considering Ampearian loop at the centre of toroid:
$\int \overrightarrow{B . d l}=\mu_0 N I$
Since, $B$ has radial symmetry $\&$ angle between $B \& d l$ is zero
$\begin{aligned} & \therefore B \int d l=B 2 \pi\left\{\frac{r_1+r_2}{2}\right\}=\mu_0 N I \\ & \Rightarrow B=\left[\frac{\mu_0 N I}{\pi\left(r_1+r_2\right)}\right]\end{aligned}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.