Search any question & find its solution
Question:
Answered & Verified by Expert
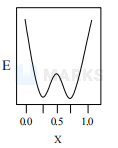
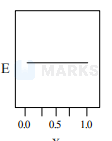
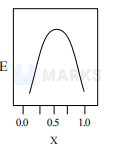
A total charge $q$ is divided as $q_{1}$ and $q_{2}$ which are kept at two of the vertices of an equilateral triangle of side a. The magnitude of the electric field $E$ at the third vertex of the triangle is to be depicted schematically as a function of $x=q_{1} / q$. Choose the correct figure.
Options:
Solution:
1735 Upvotes
Verified Answer
The correct answer is:
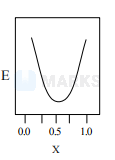

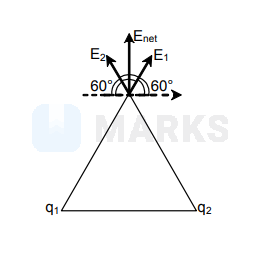
$\begin{array}{l}E_{n e t}=\vec{E}_{1}+\vec{E}_{2} \\ q=q_{1}+q_{2} \\ \left|\vec{E}_{\text {net }}\right|=\sqrt{\left(\frac{k q_{1}}{a}\right)^{2}+\left(\frac{k q_{2}}{a}\right)^{2}+\frac{2 k^{2} q_{1} q_{2}}{a^{2}} \cdot \cos 60^{\circ}} \\ E_{n e t}=\frac{k}{a} \sqrt{q_{1}^{2}+q_{2}^{2}+q_{1} q_{2}} \\ E_{n e t}=\frac{k}{a} \sqrt{q_{1}^{2}+\left(q-q_{1}\right)^{2}+q_{1}\left(q-q_{1}\right)} \\ \end{array}$
$\begin{aligned}
&=\frac{k}{a q} \times \sqrt{\left(\frac{q_{1}}{q}\right)^{2}+1^{2}+\left(\frac{q_{1}}{q}\right)^{2}-\frac{2 q_{1}}{q}+\frac{q_{1}}{q}-\frac{q_{1}^{2}}{q^{2}}} \\
&=\frac{k}{a q} \sqrt{x^{2}+1-x} \\
E_{n e t} &=\frac{k}{a q}\left(\sqrt{(x-1 / 2)^{2}+3 / 4}\right)
\end{aligned}$
Minima must be at $|\mathrm{x}=1 / 2|$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.