Search any question & find its solution
Question:
Answered & Verified by Expert
A tower, of $x$ metres high, has a flagstaff at its top. The tower and the flagstaff subtend equal angles at a point distant $y$ metres from the foot of the tower. Then, the length of the flagstaff (in metres), is
Options:
Solution:
2619 Upvotes
Verified Answer
The correct answer is:
$\frac{x\left(y^2+x^2\right)}{\left(y^2-x^2\right)}$
Let $B C$ be the height of tower and $C D$ be height of the flagstaff,
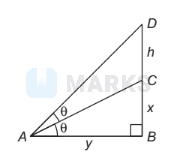
Let
$C D=h$
Since, the tower and flagstaff makes equal angle, i.e. $\theta$ In $\triangle B A C$,

In $\triangle D A B$,
$\begin{aligned}
\tan 2 \theta & =\frac{x+h}{y} \\
\Rightarrow \quad \frac{2 \tan \theta}{1-\tan ^2 \theta} & =\frac{x+h}{y} \\
\Rightarrow \quad \frac{2\left(\frac{x}{y}\right)}{1-\frac{x^2}{y^2}} & =\frac{x+h}{y} \\
\Rightarrow \quad 2 x y^2 & =\left(y^2-x^2\right)(x+h) \\
\Rightarrow \quad & \text { [from Eq. (i)] } \\
\Rightarrow \quad x^2+x^3 & =\left(y^2-x^2\right) h \\
h & =\frac{x\left(x^2+y^2\right)}{\left(y^2-x^2\right)}
\end{aligned}$

Let
$C D=h$
Since, the tower and flagstaff makes equal angle, i.e. $\theta$ In $\triangle B A C$,

In $\triangle D A B$,
$\begin{aligned}
\tan 2 \theta & =\frac{x+h}{y} \\
\Rightarrow \quad \frac{2 \tan \theta}{1-\tan ^2 \theta} & =\frac{x+h}{y} \\
\Rightarrow \quad \frac{2\left(\frac{x}{y}\right)}{1-\frac{x^2}{y^2}} & =\frac{x+h}{y} \\
\Rightarrow \quad 2 x y^2 & =\left(y^2-x^2\right)(x+h) \\
\Rightarrow \quad & \text { [from Eq. (i)] } \\
\Rightarrow \quad x^2+x^3 & =\left(y^2-x^2\right) h \\
h & =\frac{x\left(x^2+y^2\right)}{\left(y^2-x^2\right)}
\end{aligned}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.