Search any question & find its solution
Question:
Answered & Verified by Expert
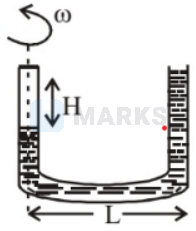
A U - shaped tube contains a liquid of density rho and it is rotated about the left dotted line as shown in the figure. Find the difference in the levels of liquid column.
Options:

Solution:
2527 Upvotes
Verified Answer
The correct answer is:
$\frac{\omega^{2} \mathrm{~L}^{2}}{2 g}$
Weight of liquid of height \(\mathrm{H}=\frac{\pi \mathrm{d}^{2}}{4} \times \mathrm{H} \rho \times \mathrm{g} \rightarrow\) (i)
Let us consider a mass dm situated at a distance \(x\) from \(A\) as shown in the figure. The centripetal force required for the mass to rotate \(=(\mathrm{dm}) \omega^{2}\)
\(\therefore\) The total centripetal force required for the mass of length \(L\) to rotate \(=\int_{0}^{1}\left(\rho \mathrm{x} \frac{\pi \mathrm{d}^{2}}{4}\right) \mathrm{xdx} \times\left(\mathrm{x} \omega^{2}\right)=\rho \times \frac{\pi \mathrm{d}^{2}}{4} \times \omega^{2} \times \frac{1^{2}}{2} \rightarrow\) (ii)
This centripetal force required is provided by the weight of liquid of height 'H' From (i) and (ii)
\(\begin{aligned} & \frac{\pi \mathrm{d}^{2}}{4} \times \mathrm{H} \times \rho \times \mathrm{g}=\rho \times \frac{\pi \mathrm{d}^{2}}{4} \times \omega^{2} \times \frac{1^{2}}{2} \\ & \Rightarrow \mathrm{H}=\frac{\omega^{2} \mathrm{l}^{2}}{2 \mathrm{~g}} \end{aligned}\)

Let us consider a mass dm situated at a distance \(x\) from \(A\) as shown in the figure. The centripetal force required for the mass to rotate \(=(\mathrm{dm}) \omega^{2}\)
\(\therefore\) The total centripetal force required for the mass of length \(L\) to rotate \(=\int_{0}^{1}\left(\rho \mathrm{x} \frac{\pi \mathrm{d}^{2}}{4}\right) \mathrm{xdx} \times\left(\mathrm{x} \omega^{2}\right)=\rho \times \frac{\pi \mathrm{d}^{2}}{4} \times \omega^{2} \times \frac{1^{2}}{2} \rightarrow\) (ii)
This centripetal force required is provided by the weight of liquid of height 'H' From (i) and (ii)
\(\begin{aligned} & \frac{\pi \mathrm{d}^{2}}{4} \times \mathrm{H} \times \rho \times \mathrm{g}=\rho \times \frac{\pi \mathrm{d}^{2}}{4} \times \omega^{2} \times \frac{1^{2}}{2} \\ & \Rightarrow \mathrm{H}=\frac{\omega^{2} \mathrm{l}^{2}}{2 \mathrm{~g}} \end{aligned}\)

Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.