Search any question & find its solution
Question:
Answered & Verified by Expert
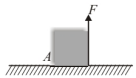
A uniform cube of mass $m$ and side $a$ is placed on a frictionless horizontal surface. A vertical force $F$ is applied to the edge as shown in figure. Match the following (most appropriate choice)
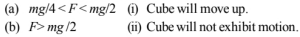
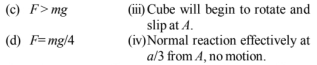

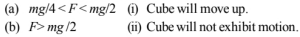
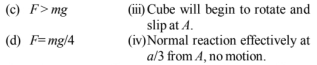
Solution:
1219 Upvotes
Verified Answer
Let us consider the given diagram.
Moment of the force due to $F$ about point is anticlockwise $A, \tau_1=\vec{F} \times a$
Moment of force due to weight $m g$ of the cube about point $A$ is clockwise
$\tau_2=m g \times \frac{a}{2}$
(i) Cube will not move or exhibit motion, if $\tau_1=\tau_2$
( $\because$ In this case, both the torque will cancel the effect of each other)
$$
\therefore \vec{F} \times a=m g \times \frac{a}{2} \Rightarrow F=\frac{m g}{2} \text { so (a) } \rightarrow \text { (ii) }
$$
(ii) Cube will rotate if, $\tau_1>\tau_2$
$$
\vec{F} \times a>m g \times \frac{a}{2} \Rightarrow F>\frac{m g}{2} \text { so (b) } \rightarrow \text { (iii) }
$$
(iii) If normal reaction is effectively acting at $\frac{a}{3}$ from point $A$, then
Torque due to $m g, \tau_2=m g \times \frac{a}{3}$
Torque due to $F$ is, $\tau_1=F \times a$
(For no motion)
So, $\tau_1=\tau_2 \Rightarrow F \cdot a=m g\left(\frac{a}{3}\right)$
If $F>m g$, block move upside, (c) $\rightarrow$ (i)
(iv) If $F=\frac{m g}{4}$ which is less than $\frac{m g}{3}$, or $\left(\frac{m g}{3}\right)>\left(\frac{m g}{4}\right)$ So due to $F=\frac{m g}{4}$, block will not move. (d) $\rightarrow$ (iv) there will be no motion.
$\therefore$ (a) $\rightarrow$ (ii), (b) $\rightarrow$ (iii), (c) $\rightarrow$ (i), (d) $\rightarrow$ (iv)
Moment of the force due to $F$ about point is anticlockwise $A, \tau_1=\vec{F} \times a$
Moment of force due to weight $m g$ of the cube about point $A$ is clockwise
$\tau_2=m g \times \frac{a}{2}$

(i) Cube will not move or exhibit motion, if $\tau_1=\tau_2$
( $\because$ In this case, both the torque will cancel the effect of each other)
$$
\therefore \vec{F} \times a=m g \times \frac{a}{2} \Rightarrow F=\frac{m g}{2} \text { so (a) } \rightarrow \text { (ii) }
$$
(ii) Cube will rotate if, $\tau_1>\tau_2$
$$
\vec{F} \times a>m g \times \frac{a}{2} \Rightarrow F>\frac{m g}{2} \text { so (b) } \rightarrow \text { (iii) }
$$
(iii) If normal reaction is effectively acting at $\frac{a}{3}$ from point $A$, then
Torque due to $m g, \tau_2=m g \times \frac{a}{3}$
Torque due to $F$ is, $\tau_1=F \times a$
(For no motion)
So, $\tau_1=\tau_2 \Rightarrow F \cdot a=m g\left(\frac{a}{3}\right)$
If $F>m g$, block move upside, (c) $\rightarrow$ (i)
(iv) If $F=\frac{m g}{4}$ which is less than $\frac{m g}{3}$, or $\left(\frac{m g}{3}\right)>\left(\frac{m g}{4}\right)$ So due to $F=\frac{m g}{4}$, block will not move. (d) $\rightarrow$ (iv) there will be no motion.
$\therefore$ (a) $\rightarrow$ (ii), (b) $\rightarrow$ (iii), (c) $\rightarrow$ (i), (d) $\rightarrow$ (iv)
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.