Search any question & find its solution
Question:
Answered & Verified by Expert
A uniform disc of radius $R$, is resting on a table on its rim. The coefficient of friction between disc and table is $\mu$ (figure). Now, the disc is pulled with a force $F$ as shown in the figure. What is the maximum value of $F$ for which the disc rolls without slipping?
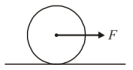

Solution:
2115 Upvotes
Verified Answer
As the given diagram,
Frictional force $(f)$ is acting in the opposite direction of $F$. Let us consider ' $a$ ' and $\alpha$ be the linear and angular acceleration respectively. So, the acceleration of centre of mass of disc for linear motion,
$$
F-f=M a
$$
where $M$ is mass of the disc.
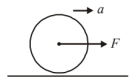
Force of friction $(f)$ applies torque about centre $O$. But torque due to $F$ is zero, as $F$ is along ' $O$ '.
The angular acceleration of the disc is
$$
\alpha=a / R \quad \text { (for pure rolling) }
$$
Torque on disc, $\tau=I_D \alpha$
M.I. of disc is $I_D=\frac{1}{2} M R^2$
$$
\begin{aligned}
&f R=\left(\frac{1}{2} M R^2\right) \alpha \\
&\Rightarrow f R=\left(\frac{1}{2} M R^2\right)\left(\frac{a}{R}\right)=\frac{1}{2} M R a \quad\left(\because \alpha=\frac{a}{R}\right) \\
&M a=2 f \ldots \text { (ii) }
\end{aligned}
$$
From eqs. (i) and (ii), we get
$$
F-f=2 f \Rightarrow F=3 f
$$
$$
f=\frac{F}{3} \quad(\because f=\mu N=\mu M g, N=M g)
$$
$$
\begin{aligned}
&\frac{F}{3}=\mu M g \Rightarrow F=3 \mu M g \\
&F_{\max }=3 \mu M g
\end{aligned}
$$
Hence, $F_{\max }=3 \mu \mathrm{Mg}$ is the maximum force applied on disc to roll on surface without slipping.
Frictional force $(f)$ is acting in the opposite direction of $F$. Let us consider ' $a$ ' and $\alpha$ be the linear and angular acceleration respectively. So, the acceleration of centre of mass of disc for linear motion,
$$
F-f=M a
$$
where $M$ is mass of the disc.

Force of friction $(f)$ applies torque about centre $O$. But torque due to $F$ is zero, as $F$ is along ' $O$ '.
The angular acceleration of the disc is
$$
\alpha=a / R \quad \text { (for pure rolling) }
$$
Torque on disc, $\tau=I_D \alpha$
M.I. of disc is $I_D=\frac{1}{2} M R^2$
$$
\begin{aligned}
&f R=\left(\frac{1}{2} M R^2\right) \alpha \\
&\Rightarrow f R=\left(\frac{1}{2} M R^2\right)\left(\frac{a}{R}\right)=\frac{1}{2} M R a \quad\left(\because \alpha=\frac{a}{R}\right) \\
&M a=2 f \ldots \text { (ii) }
\end{aligned}
$$
From eqs. (i) and (ii), we get
$$
F-f=2 f \Rightarrow F=3 f
$$
$$
f=\frac{F}{3} \quad(\because f=\mu N=\mu M g, N=M g)
$$
$$
\begin{aligned}
&\frac{F}{3}=\mu M g \Rightarrow F=3 \mu M g \\
&F_{\max }=3 \mu M g
\end{aligned}
$$
Hence, $F_{\max }=3 \mu \mathrm{Mg}$ is the maximum force applied on disc to roll on surface without slipping.
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.