Search any question & find its solution
Question:
Answered & Verified by Expert
A uniform rod $\mathrm{AB}$ of length $I$ and mass $m$ is free to rotate about point $A$. The rod is released from rest in the horizontal position. Given that the moment of inertia of the rod about $\mathrm{A}$ is $m l^2 / 3$, the initial angular acceleration of the rod will be
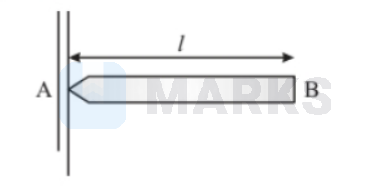
Options:

Solution:
2110 Upvotes
Verified Answer
The correct answer is:
$\frac{3 g}{2 l}$
Given that moment of inertia about \(A\) is
\(I=m l^3 / 3\)
Now, torque about \(A\) is given as
\(\begin{aligned}
& \tau=F \times r \\
& \tau=m g \frac{1}{2} \\
& I \alpha=m g \frac{1}{2} \\
& \frac{m l^2}{3} \alpha=m g \frac{1}{2} \\
& \alpha=\frac{3 g}{2 l}
\end{aligned}\)
\(I=m l^3 / 3\)
Now, torque about \(A\) is given as
\(\begin{aligned}
& \tau=F \times r \\
& \tau=m g \frac{1}{2} \\
& I \alpha=m g \frac{1}{2} \\
& \frac{m l^2}{3} \alpha=m g \frac{1}{2} \\
& \alpha=\frac{3 g}{2 l}
\end{aligned}\)
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.