Search any question & find its solution
Question:
Answered & Verified by Expert
A uniform rod of length $60 \mathrm{~cm}$ is placed with one end in contact with the horizontal table and is then inclined at an angle $30^{\circ}$ to the horizontal and allowed to fall. The angular velocity of the rod when it becomes horizontal is (acceleration due to gravity $=10 \mathrm{~ms}^{-2}$ )
Options:
Solution:
2898 Upvotes
Verified Answer
The correct answer is:
$5 \mathrm{rad} \mathrm{s}^{-1}$
( As rod falls, its loss of gravitational potential energy appears as gain of angular rotational energy.
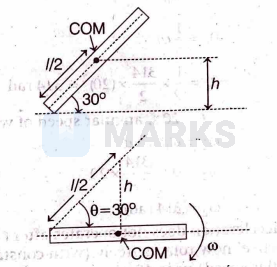
If rod is rotating at angular speed $\omega$ when it is horizontal then,
Rotational K E = Loss of gravitational PE
$$
\Rightarrow \quad \frac{1}{2} I \omega^2=m g h
$$
Now for rod,
Moment of inertia of a solid rod about its one end,
$$
I=\frac{M L^2}{3}
$$
and $h=\frac{l}{2} \sin \theta$ (see figure $\theta=30^{\circ}$ )
$$
=\frac{l}{2} \times \frac{1}{2}=\frac{l}{4}
$$
So from eq. (i), we have
$$
\frac{1}{2} M \frac{l^2}{3} \times \omega^2=M g \frac{l}{4}
$$
$$
\Rightarrow
$$
$$
\omega^2=\frac{3}{2} \times \frac{g}{l}
$$
Here, $g=10 \mathrm{~m} / \mathrm{s}^2$ and $l=0.6 \mathrm{~m}$
So, $\omega^2=\frac{3}{2} \times \frac{10}{0.6}=25$
or $\quad \omega=5 \mathrm{rad} / \mathrm{s}$

If rod is rotating at angular speed $\omega$ when it is horizontal then,
Rotational K E = Loss of gravitational PE
$$
\Rightarrow \quad \frac{1}{2} I \omega^2=m g h
$$
Now for rod,
Moment of inertia of a solid rod about its one end,
$$
I=\frac{M L^2}{3}
$$
and $h=\frac{l}{2} \sin \theta$ (see figure $\theta=30^{\circ}$ )
$$
=\frac{l}{2} \times \frac{1}{2}=\frac{l}{4}
$$
So from eq. (i), we have
$$
\frac{1}{2} M \frac{l^2}{3} \times \omega^2=M g \frac{l}{4}
$$
$$
\Rightarrow
$$
$$
\omega^2=\frac{3}{2} \times \frac{g}{l}
$$
Here, $g=10 \mathrm{~m} / \mathrm{s}^2$ and $l=0.6 \mathrm{~m}$
So, $\omega^2=\frac{3}{2} \times \frac{10}{0.6}=25$
or $\quad \omega=5 \mathrm{rad} / \mathrm{s}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.