Search any question & find its solution
Question:
Answered & Verified by Expert
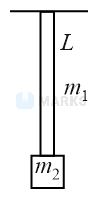
A uniform rope of length and mass , hangs vertically from a rigid support. A block of mass is attached to the free end of the rope. A transverse pulse of wavelength is produced at the lower end of the rope. The wavelength of the pulse when it reaches the top of the rope is . The ratio is:
Options:
Solution:
1428 Upvotes
Verified Answer
The correct answer is:
The situation in the rope is given below,
The velocity of the wave at the bottom of the rope is given by,
; where is tension and is linear mass density of the string.
Hence, the wavelength for frequency will be,
Similarly, at top the velocity will be,
And, the wavelength will be,
Hence, the ratio of both wavelengths will be,
.
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.