Search any question & find its solution
Question:
Answered & Verified by Expert
A U-tube in which the cross-sectional area of the limb on the left is one quarter, the limb on the right contains mercury (density $13.6 \mathrm{~g} / \mathrm{cm}^3$ ). The level of mercury in the narrow limb is at a distance of $36 \mathrm{~cm}$ from the upper end of the tube. What will be the rise in the level of mercury in the right limb if the left limb is filled to the top with water
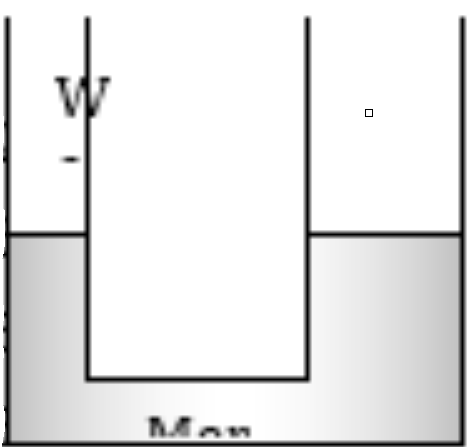
Options:

Solution:
1163 Upvotes
Verified Answer
The correct answer is:
$0.56 \mathrm{~cm}$
If the rise of level in the right limb be $x \mathrm{~cm}$. the fall of level of mercury in left limb be $4 \times \mathrm{cm}$ because the area of cross section of right limb is 4 times as that of left limb.
$\therefore$ Level of water in left limb is $(36+4 x) \mathrm{cm}$.
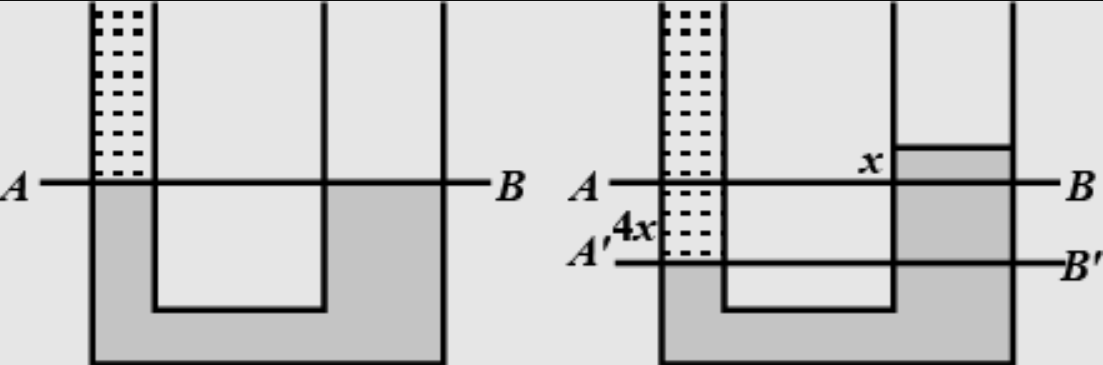
Now equating pressure at interface of Fig and water $r\left(\right.$ at $\left.A^{\prime} B^{\prime}\right)$
$(36+4 x) \times 1 \times g=5 x \times 13.6 \times g$
By solving we get $x=0.56 \mathrm{~cm}$.
$\therefore$ Level of water in left limb is $(36+4 x) \mathrm{cm}$.

Now equating pressure at interface of Fig and water $r\left(\right.$ at $\left.A^{\prime} B^{\prime}\right)$
$(36+4 x) \times 1 \times g=5 x \times 13.6 \times g$
By solving we get $x=0.56 \mathrm{~cm}$.
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.