Search any question & find its solution
Question:
Answered & Verified by Expert
A variable plane is at a constant distance $h$ from the origin and meets the coordinate axes in $A, B, C$. Locus of centroid of $A B C$ is
Options:
Solution:
2484 Upvotes
Verified Answer
The correct answer is:
$\frac{1}{x^2}+\frac{1}{y^2}+\frac{1}{z^2}=\frac{9}{h^2}$
The centroid of the triangle is $C\left(\frac{a}{3}, \frac{b}{3}, \frac{c}{3}\right)$
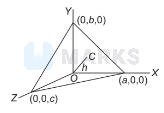
The direction coines of the line $O C$ are $\left(\frac{h}{a}, \frac{h}{b}, \frac{h}{c}\right)$.
As we know that,
$\begin{array}{rlrl} & l^2+m^2+n^2 & =1 \\ \Rightarrow & & \frac{h^2}{a^2}+\frac{h^2}{b^2}+\frac{h^2}{c^2} & =1 \\ \Rightarrow & & \frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2} & =\frac{1}{h^2} \\ \Rightarrow & & \left(\frac{3}{a}\right)^2+\left(\frac{3}{b}\right)^2+\left(\frac{3}{c}\right)^2 & =\frac{9}{h^2}\end{array}$
The locus of the centroid is
$\frac{1}{x^2}+\frac{1}{y^2}+\frac{1}{z^2}=\frac{9}{h^2}$

The direction coines of the line $O C$ are $\left(\frac{h}{a}, \frac{h}{b}, \frac{h}{c}\right)$.
As we know that,
$\begin{array}{rlrl} & l^2+m^2+n^2 & =1 \\ \Rightarrow & & \frac{h^2}{a^2}+\frac{h^2}{b^2}+\frac{h^2}{c^2} & =1 \\ \Rightarrow & & \frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2} & =\frac{1}{h^2} \\ \Rightarrow & & \left(\frac{3}{a}\right)^2+\left(\frac{3}{b}\right)^2+\left(\frac{3}{c}\right)^2 & =\frac{9}{h^2}\end{array}$
The locus of the centroid is
$\frac{1}{x^2}+\frac{1}{y^2}+\frac{1}{z^2}=\frac{9}{h^2}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.