Search any question & find its solution
Question:
Answered & Verified by Expert
A wire of length $l$ and mass $m$ is bent in the form of a semicircle. The gravitational field intensity at the centre of semicircle is
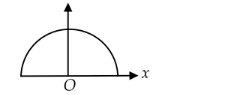
Options:

Solution:
1382 Upvotes
Verified Answer
The correct answer is:
$\frac{2 \pi G m}{l^2}$ along $y$-axis
Consider two small elements each of length $d l=r d \theta$ symmetrically.
$\pi r=l$
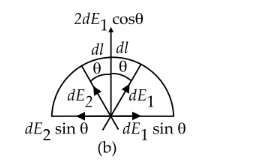
Resolve the elemental field intensities
$\because\left|d E_1\right|=\left|d E_2\right|$
$d E=2 d E_1 \cos \theta=\frac{2 G r d \theta}{r^2} \cos \theta$
$\begin{aligned} & \mathrm{G}=\text { Gravitational constant } \\ & \lambda=\text { Linear massdensity }=\frac{m}{l}\end{aligned}$
or $d E=\frac{2 \lambda G}{r} \int_0^{90^{\circ}} \cos \theta d \theta=\frac{2 \lambda G}{r}=\frac{2 \pi G m}{l^2}$
$\pi r=l$
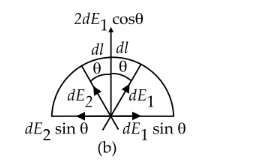
Resolve the elemental field intensities
$\because\left|d E_1\right|=\left|d E_2\right|$
$d E=2 d E_1 \cos \theta=\frac{2 G r d \theta}{r^2} \cos \theta$
$\begin{aligned} & \mathrm{G}=\text { Gravitational constant } \\ & \lambda=\text { Linear massdensity }=\frac{m}{l}\end{aligned}$
or $d E=\frac{2 \lambda G}{r} \int_0^{90^{\circ}} \cos \theta d \theta=\frac{2 \lambda G}{r}=\frac{2 \pi G m}{l^2}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.