Search any question & find its solution
Question:
Answered & Verified by Expert
A wire of length $l$ is bent into a circular loop of radius $R$ and carries a current $I$. The magnetic field at the centre of the loop is $B$. The same wire is now bent into a double loop of equal radii. If both loops carry the same current $I$ and it is in the same direction, the magnetic field at the centre of the double loop will be
Options:
Solution:
1259 Upvotes
Verified Answer
The correct answer is:
Zero
Magnetic field at the centre of the loop
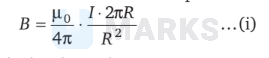
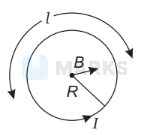
For the wire which is looped double let radius becomes $r$ Then,
$\begin{aligned}
\frac{l}{2} & =2 \pi r \\
\text{or} \quad \frac{l}{4 \pi} & =(r)
\end{aligned}$
$\begin{array}{ll}\therefore & B^{\prime}=\frac{\mu_0}{4 \pi} \cdot \frac{I \cdot 2 \pi r \times 2}{r^2} \\ \text { or } & B^{\prime}=\frac{\mu_0}{4 \pi} \cdot \frac{I \cdot \frac{l}{2} \cdot 2}{\left(\frac{l}{4 \pi}\right)^2}\end{array}$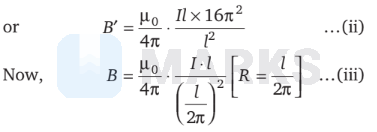
Dividing Eq. (ii) by Eq. (iii), we get
$\frac{B^{\prime}}{B}=\frac{\frac{\mu_0}{4 \pi} \cdot \frac{I \cdot l \cdot 16 \pi^2}{l^2}}{\frac{\mu_0}{4 \pi} \cdot \frac{I l \cdot 4 \pi^2}{l^2}}$
$\begin{array}{ll}\text { or } & \frac{B^{\prime}}{B}=4 \\ \text { or } & B^{\prime}=4 B\end{array}$
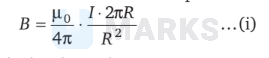

For the wire which is looped double let radius becomes $r$ Then,
$\begin{aligned}
\frac{l}{2} & =2 \pi r \\
\text{or} \quad \frac{l}{4 \pi} & =(r)
\end{aligned}$
$\begin{array}{ll}\therefore & B^{\prime}=\frac{\mu_0}{4 \pi} \cdot \frac{I \cdot 2 \pi r \times 2}{r^2} \\ \text { or } & B^{\prime}=\frac{\mu_0}{4 \pi} \cdot \frac{I \cdot \frac{l}{2} \cdot 2}{\left(\frac{l}{4 \pi}\right)^2}\end{array}$
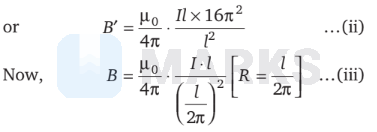
Dividing Eq. (ii) by Eq. (iii), we get
$\frac{B^{\prime}}{B}=\frac{\frac{\mu_0}{4 \pi} \cdot \frac{I \cdot l \cdot 16 \pi^2}{l^2}}{\frac{\mu_0}{4 \pi} \cdot \frac{I l \cdot 4 \pi^2}{l^2}}$
$\begin{array}{ll}\text { or } & \frac{B^{\prime}}{B}=4 \\ \text { or } & B^{\prime}=4 B\end{array}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.