Search any question & find its solution
Question:
Answered & Verified by Expert
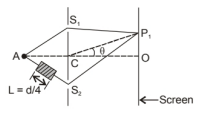
$\mathrm{AC}=\mathrm{CO}=\mathrm{D}, \mathrm{S}_1 \mathrm{C}=\mathrm{S}_2 \mathrm{C}=\mathrm{d} \ll \mathrm{D}$
A small transparent slab containing material of $\mu=1.5$ is placed along $\mathrm{AS}_2$ (figure). What will be the distance from $\mathrm{O}$ of the principal maxima and of the first minima on either side of the principal maxima obtained in the absence of the glass slab?
Solution:
1493 Upvotes
Verified Answer
When, ray pass through a transparent glass slab of thickness L of refractive index $\mu$ so the path difference caused by slab is $(\mu-1) \mathrm{L}$ and path difference caused by YDSE is $2 d \sin \mathrm{A}$. then the total path difference will be calculated as
$$
\Delta \mathrm{x}=2 \mathrm{~d} \sin \theta+(\mu-1) \mathrm{L} .
$$
In case of transparent glass slabe of refractive index $\mu$, the path difference $=2 d \sin \theta+(\mu-1) \mathrm{L}$
For the principal maxima, (path difference is zero),
So,
$$
\begin{aligned}
&\Delta \mathrm{x}=0 \\
&2 \mathrm{~d} \sin \theta_0+(\mu-1) \mathrm{L}=0 \\
&\sin \theta_0=-\frac{\mathrm{L}(\mu-1)}{2 \mathrm{~d}}=\frac{-\mathrm{L}(0.5)}{2 \mathrm{~d}} \\
&=\frac{-\mathrm{L} \times 0.5}{2 \times 4 \mathrm{~L}} \quad\left[\because \mathrm{L}=\frac{\mathrm{d}}{4} ; \mathrm{d}=4 \mathrm{~L}\right] \\
&\sin \theta_0=\frac{-1}{16}
\end{aligned}
$$
$\therefore$ For central maxima
$$
\mathrm{OP}=\mathrm{D} \tan \theta_0 \approx \mathrm{D} \sin \theta_0=\frac{-\mathrm{D}}{16}
$$
For small $\angle \theta_0, \sin \theta_0=\theta_0$ and $\tan \theta_0=\theta_0$
And for the first minima, the path difference is $\pm \frac{\lambda}{2}$
So, $2 \mathrm{~d} \sin \theta_1+(\mu-1)=\pm \frac{\lambda}{2}$
( $\because$ for both upper and lower side from 0 )
$$
\therefore 2 \mathrm{~d} \sin \theta_1+0.5 \mathrm{~L}=\pm \frac{\lambda}{2}
$$
or $\sin \theta_1=\frac{\pm \frac{\lambda}{2}-0.5 \mathrm{~L}}{2 \mathrm{~d}}=\frac{\pm \frac{\lambda}{2}-\frac{\mathrm{d}}{8}}{2 \mathrm{~d}}\left[\because \mathrm{L}=\frac{\mathrm{d}}{4}\right]$
$$
=\frac{\pm \frac{\lambda}{2}-\frac{\lambda}{8}}{2 \lambda}=\pm \frac{1}{4}-\frac{1}{16}
$$
So, the diffraction occurs if the wavelength of waves is nearly equal to the side width (d)
On the positive side $\sin \theta_1^{\prime}{ }^{+}=+\frac{1}{4}-\frac{1}{16}=\frac{3}{16}$
The first principal maxima on the positive side is at distance
$$
\begin{aligned}
\mathrm{D} \tan {\theta_1^{\prime}}_1{ }^{+} &=\mathrm{D} \frac{\sin \theta_1^{\prime+}}{\sqrt{1-\sin ^2 \theta_1^{+}}}=\mathrm{D} \frac{3}{\sqrt{16^2-3^2}} \\
&=\frac{3 \mathrm{D}}{\sqrt{247}} \text { above point } \mathrm{O}
\end{aligned}
$$
The distance of first principal minima on the negative side is $\mathrm{D} \tan \theta_1^{\prime}=\frac{\mathrm{D} \sin \theta_1^{n-}}{\sqrt{1-\sin ^2 \theta_1^{\prime \prime-}}}=\frac{\frac{-5 \mathrm{D}}{16}}{\sqrt{\frac{16^2-5^2}{16}}}$ $=\frac{-5 \mathrm{D}}{\sqrt{16^2-5^2}}=\frac{-5 \mathrm{D}}{\sqrt{231}}$ below point $\mathrm{O}$.
$$
\Delta \mathrm{x}=2 \mathrm{~d} \sin \theta+(\mu-1) \mathrm{L} .
$$
In case of transparent glass slabe of refractive index $\mu$, the path difference $=2 d \sin \theta+(\mu-1) \mathrm{L}$
For the principal maxima, (path difference is zero),
So,
$$
\begin{aligned}
&\Delta \mathrm{x}=0 \\
&2 \mathrm{~d} \sin \theta_0+(\mu-1) \mathrm{L}=0 \\
&\sin \theta_0=-\frac{\mathrm{L}(\mu-1)}{2 \mathrm{~d}}=\frac{-\mathrm{L}(0.5)}{2 \mathrm{~d}} \\
&=\frac{-\mathrm{L} \times 0.5}{2 \times 4 \mathrm{~L}} \quad\left[\because \mathrm{L}=\frac{\mathrm{d}}{4} ; \mathrm{d}=4 \mathrm{~L}\right] \\
&\sin \theta_0=\frac{-1}{16}
\end{aligned}
$$
$\therefore$ For central maxima
$$
\mathrm{OP}=\mathrm{D} \tan \theta_0 \approx \mathrm{D} \sin \theta_0=\frac{-\mathrm{D}}{16}
$$
For small $\angle \theta_0, \sin \theta_0=\theta_0$ and $\tan \theta_0=\theta_0$
And for the first minima, the path difference is $\pm \frac{\lambda}{2}$
So, $2 \mathrm{~d} \sin \theta_1+(\mu-1)=\pm \frac{\lambda}{2}$
( $\because$ for both upper and lower side from 0 )
$$
\therefore 2 \mathrm{~d} \sin \theta_1+0.5 \mathrm{~L}=\pm \frac{\lambda}{2}
$$
or $\sin \theta_1=\frac{\pm \frac{\lambda}{2}-0.5 \mathrm{~L}}{2 \mathrm{~d}}=\frac{\pm \frac{\lambda}{2}-\frac{\mathrm{d}}{8}}{2 \mathrm{~d}}\left[\because \mathrm{L}=\frac{\mathrm{d}}{4}\right]$
$$
=\frac{\pm \frac{\lambda}{2}-\frac{\lambda}{8}}{2 \lambda}=\pm \frac{1}{4}-\frac{1}{16}
$$
So, the diffraction occurs if the wavelength of waves is nearly equal to the side width (d)
On the positive side $\sin \theta_1^{\prime}{ }^{+}=+\frac{1}{4}-\frac{1}{16}=\frac{3}{16}$
The first principal maxima on the positive side is at distance
$$
\begin{aligned}
\mathrm{D} \tan {\theta_1^{\prime}}_1{ }^{+} &=\mathrm{D} \frac{\sin \theta_1^{\prime+}}{\sqrt{1-\sin ^2 \theta_1^{+}}}=\mathrm{D} \frac{3}{\sqrt{16^2-3^2}} \\
&=\frac{3 \mathrm{D}}{\sqrt{247}} \text { above point } \mathrm{O}
\end{aligned}
$$
The distance of first principal minima on the negative side is $\mathrm{D} \tan \theta_1^{\prime}=\frac{\mathrm{D} \sin \theta_1^{n-}}{\sqrt{1-\sin ^2 \theta_1^{\prime \prime-}}}=\frac{\frac{-5 \mathrm{D}}{16}}{\sqrt{\frac{16^2-5^2}{16}}}$ $=\frac{-5 \mathrm{D}}{\sqrt{16^2-5^2}}=\frac{-5 \mathrm{D}}{\sqrt{231}}$ below point $\mathrm{O}$.
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.