Search any question & find its solution
Question:
Answered & Verified by Expert
An aeroplane can carry a maximum of 200 passengers. A profit of $₹ \mathbf{1 0 0 0}$ is made on each executive class ticket and a profit of $₹ 600$ is made on each economy class ticket. The airline reserves at least 20 seats for executive class. However, at least 4 times as many passengers prefer to travel by economy class than by the executive class. Determine how many tickets of each type must be sold in order to maximise the profit for the airline. What is the maximum profit?
Solution:
2222 Upvotes
Verified Answer
Let the executive class air tickets and economy class tickets sold be $\mathrm{x}$ and $\mathrm{y}$.
$\therefore \quad$ L.P.P is i.e., maximize, $(\mathrm{Z})=1000 \mathrm{x}+600 \mathrm{y}$, subject to constraints are $x+y \leq 200, x \geq 20$,
$y \geq 4 x$ and $x, y \geq 0$.
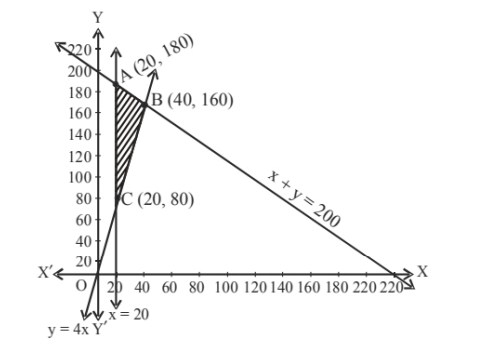
The region satisfying the inequality
$x+y \leq 200, x \geq 20$ and $y \geq 4 x$ is $A B C$.
$\mathrm{Z}=1000 \mathrm{x}+600 \mathrm{y}$
At A $(20,180), \mathrm{Z}=1000 \times 20+600 \times 180$
$=20000+108000=128000$
At $\mathrm{B}(40,160), \mathrm{Z}=1000 \times 40+600 \times 160$
$=40000+96000=136000 \max ^{\mathrm{m}}$
At $\mathrm{C}(20,80), \quad \mathrm{Z}=1000 \times 20+600 \times 80$
$=20000+48000=68000$
$\Rightarrow \mathrm{Z}$ is maximum when $\mathrm{x}=40, \mathrm{y}=160$
$\Rightarrow 40$ tickets of executive class and 160 tickets of economy class should be sold to get the maximum profit of $₹ 13600$.
$\therefore \quad$ L.P.P is i.e., maximize, $(\mathrm{Z})=1000 \mathrm{x}+600 \mathrm{y}$, subject to constraints are $x+y \leq 200, x \geq 20$,
$y \geq 4 x$ and $x, y \geq 0$.
The region satisfying the inequality
$x+y \leq 200, x \geq 20$ and $y \geq 4 x$ is $A B C$.
$\mathrm{Z}=1000 \mathrm{x}+600 \mathrm{y}$
At A $(20,180), \mathrm{Z}=1000 \times 20+600 \times 180$
$=20000+108000=128000$
At $\mathrm{B}(40,160), \mathrm{Z}=1000 \times 40+600 \times 160$
$=40000+96000=136000 \max ^{\mathrm{m}}$
At $\mathrm{C}(20,80), \quad \mathrm{Z}=1000 \times 20+600 \times 80$
$=20000+48000=68000$

$\Rightarrow \mathrm{Z}$ is maximum when $\mathrm{x}=40, \mathrm{y}=160$
$\Rightarrow 40$ tickets of executive class and 160 tickets of economy class should be sold to get the maximum profit of $₹ 13600$.
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.