Search any question & find its solution
Question:
Answered & Verified by Expert
An electron in an electron microscope with initial velocity $v_{0} \hat{i}$ enters a region of a stray transverse electric field $\mathrm{E}_{0} \hat{\mathrm{j}}$. The time taken for the change in its de-Broglie wavelength from the initial value of $\lambda$ to $\lambda / 3$ is proportional to
Options:
Solution:
1489 Upvotes
Verified Answer
The correct answer is:
$\frac{1}{\mathrm{E}_{0}}$
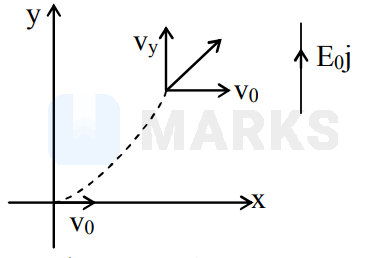
$\lambda=\frac{\mathrm{h}}{\mathrm{mv}} \Rightarrow \lambda \propto \frac{1}{\mathrm{v}}$
$\mathrm{v}=\sqrt{\mathrm{v}_{\mathrm{y}}^{2}+\mathrm{v}_{0}^{2}}$
$\mathrm{v}_{\mathrm{y}}=\mathrm{u}_{\mathrm{y}}+\mathrm{a}_{\mathrm{y}} \mathrm{t}$
$\mathrm{v}_{\mathrm{y}}=0+\frac{\mathrm{qE}_{0}}{\mathrm{~m}} \mathrm{t}$
$\left(3 \mathrm{v}_{0}\right)=\sqrt{\mathrm{v}_{\mathrm{y}}^{2}+\mathrm{v}_{0}^{2}}$
$\Rightarrow \mathrm{v}_{\mathrm{y}}^{2}=8 \mathrm{v}_{0}^{2}$
$\Rightarrow \frac{\mathrm{qE}_{0}}{\mathrm{~m}} \mathrm{t}=2 \sqrt{2} \mathrm{v}_{0}$
$\quad \mathrm{t}=\frac{2 \sqrt{2} \mathrm{~m}}{\mathrm{q} \mathrm{E}_{0}} \mathrm{v}_{0} \Rightarrow \mathrm{t} \propto \frac{1}{\mathrm{E}_{0}}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.