Search any question & find its solution
Question:
Answered & Verified by Expert
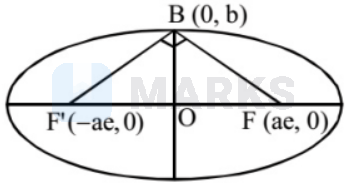
An ellipse has $\mathrm{OB}$ as semi minor axis, $\mathrm{F}$ and $\mathrm{F}^{\prime}$ its focii and the angle FBF' is a right angle. Then the eccentricity of the ellipse is
Options:
Solution:
1199 Upvotes
Verified Answer
The correct answer is:
$\frac{1}{\sqrt{2}}$
$\because \angle \mathrm{FBF}^{\prime}=90^{\circ}$
$\Rightarrow \mathrm{FB}^{2}+\mathrm{F}^{\prime} \mathrm{B}^{2}=\mathrm{FF}^{\prime 2}$
$\therefore\left(\sqrt{a^{2} e^{2}+b^{2}}\right)^{2}+\left(\sqrt{a^{2} e^{2}+b^{2}}\right)^{2}=(2 a e)^{2}$
$\Rightarrow 2\left(a^{2} e^{2}+b^{2}\right)=4 a^{2} e^{2}$
$\Rightarrow e^{2}=\frac{b^{2}}{a^{2}}$
Also $e^{2}=1-\frac{b^{2}}{a^{2}}=1-e^{2}$
$\begin{array}{l}
\Rightarrow 2 e^{2}=1 \\
\Rightarrow e=\frac{1}{\sqrt{2}}
\end{array}$
$\Rightarrow \mathrm{FB}^{2}+\mathrm{F}^{\prime} \mathrm{B}^{2}=\mathrm{FF}^{\prime 2}$
$\therefore\left(\sqrt{a^{2} e^{2}+b^{2}}\right)^{2}+\left(\sqrt{a^{2} e^{2}+b^{2}}\right)^{2}=(2 a e)^{2}$
$\Rightarrow 2\left(a^{2} e^{2}+b^{2}\right)=4 a^{2} e^{2}$
$\Rightarrow e^{2}=\frac{b^{2}}{a^{2}}$

Also $e^{2}=1-\frac{b^{2}}{a^{2}}=1-e^{2}$
$\begin{array}{l}
\Rightarrow 2 e^{2}=1 \\
\Rightarrow e=\frac{1}{\sqrt{2}}
\end{array}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.