Search any question & find its solution
Question:
Answered & Verified by Expert
An empty tank has concave mirror as its bottom. When sunlight falls normally on the mirror, it is focussed at a height of $32 \mathrm{~cm}$ from the mirror. If the tank is filled with water upto a height of $20 \mathrm{~cm}$, then the sunlight focusses at (refractive index of water $=\frac{4}{3}$ )
Options:
Solution:
1550 Upvotes
Verified Answer
The correct answer is:
$9 \mathrm{~cm}$ above water level
Sun at infinity, $u=\infty$
Focussed at a height, $\mathrm{v}=-32 \mathrm{~cm}$
Refractive index of water, $\mu_{\mathrm{w}}=\frac{4}{3}$
From the mirror formula
$\begin{aligned}
& \frac{1}{\mathrm{f}}=\frac{1}{\mathrm{v}}+\frac{1}{\mathrm{u}} \Rightarrow \frac{1}{\mathrm{f}}=\frac{1}{32}+\frac{1}{\infty} \\
& \Rightarrow \mathrm{f}=-32 \mathrm{~cm}
\end{aligned}$
When water is filled in the tank upto a height of $20 \mathrm{~cm}$, the image formed by the mirror will act as virtual object for water surface.
Which will form its image such that
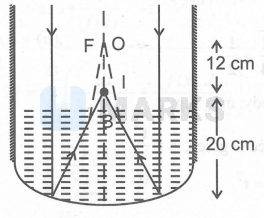
$\begin{aligned} & \frac{\text { Actual height }}{\text { Apparent height }}=\frac{\mu_{\mathrm{w}}}{\mu_{\mathrm{a}}} \\ & \frac{\mathrm{BO}}{\mathrm{BI}}=\frac{4 / 3}{1} \\ & \Rightarrow \mathrm{BI}=\mathrm{BO} \times \frac{3}{4} \\ & =12 \times \frac{3}{4}=9 \mathrm{~cm} \text { above water level }\end{aligned}$
Focussed at a height, $\mathrm{v}=-32 \mathrm{~cm}$
Refractive index of water, $\mu_{\mathrm{w}}=\frac{4}{3}$
From the mirror formula
$\begin{aligned}
& \frac{1}{\mathrm{f}}=\frac{1}{\mathrm{v}}+\frac{1}{\mathrm{u}} \Rightarrow \frac{1}{\mathrm{f}}=\frac{1}{32}+\frac{1}{\infty} \\
& \Rightarrow \mathrm{f}=-32 \mathrm{~cm}
\end{aligned}$
When water is filled in the tank upto a height of $20 \mathrm{~cm}$, the image formed by the mirror will act as virtual object for water surface.
Which will form its image such that

$\begin{aligned} & \frac{\text { Actual height }}{\text { Apparent height }}=\frac{\mu_{\mathrm{w}}}{\mu_{\mathrm{a}}} \\ & \frac{\mathrm{BO}}{\mathrm{BI}}=\frac{4 / 3}{1} \\ & \Rightarrow \mathrm{BI}=\mathrm{BO} \times \frac{3}{4} \\ & =12 \times \frac{3}{4}=9 \mathrm{~cm} \text { above water level }\end{aligned}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.