Search any question & find its solution
Question:
Answered & Verified by Expert
An inductor coil is connected to a capacitor and an AC source of rms voltage $8 \mathrm{~V}$ in series. The rms current in the circuit is $16 \mathrm{~A}$ and is in phase with emf. If this inductor coil is connected to $6 \mathrm{~V}$ DC battery, the magnitude of steady current is
Options:
Solution:
1015 Upvotes
Verified Answer
The correct answer is:
$12 \mathrm{~A}$
Given, rms voltage of AC source $V_{\text {rms }}=8 \mathrm{~V}$ and the rms current in the circuit, $I_{\mathrm{rms}}=16 \mathrm{~A}$ According to the question,
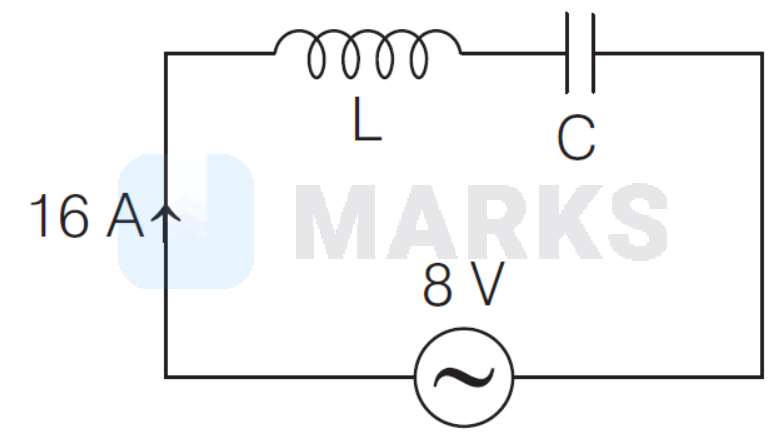
$\therefore$ Impedance of the circuit,
$$
\begin{aligned}
& Z=\frac{V_{\mathrm{rms}}}{I_{\mathrm{rms}}}=\frac{8}{16} \\
& Z=0.5 \Omega
\end{aligned}
$$
When the inductor coil is comected to a $6 \mathrm{~V} D C$ battery then $V_{\text {rms }}^{\prime}=6 \mathrm{~V}=V_{D C}$
$\therefore$ Magnitude of steady current,
$$
I^{\prime}=\frac{V_{\text {rms }}^{\prime}}{Z}=\frac{6}{0.5}=12 \mathrm{~A}
$$

$\therefore$ Impedance of the circuit,
$$
\begin{aligned}
& Z=\frac{V_{\mathrm{rms}}}{I_{\mathrm{rms}}}=\frac{8}{16} \\
& Z=0.5 \Omega
\end{aligned}
$$
When the inductor coil is comected to a $6 \mathrm{~V} D C$ battery then $V_{\text {rms }}^{\prime}=6 \mathrm{~V}=V_{D C}$
$\therefore$ Magnitude of steady current,
$$
I^{\prime}=\frac{V_{\text {rms }}^{\prime}}{Z}=\frac{6}{0.5}=12 \mathrm{~A}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.