Search any question & find its solution
Question:
Answered & Verified by Expert
An infinite number of masses are placed on a frictionless table and they are connected via massless strings. Their masses follow the sequence, $m, \frac{m}{2}, \frac{m}{6}, \ldots \ldots \ldots . . . \frac{m}{n !}, \ldots \ldots . .$. and they are further connected to a mass $m$ that hangs over a massless pulley. The acceleration of the hanging mass is
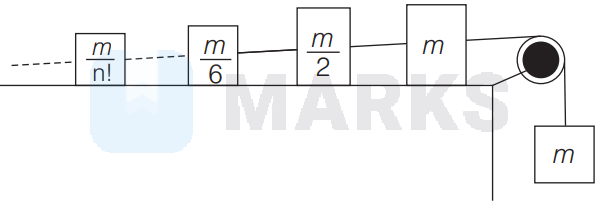
Options:

Solution:
1964 Upvotes
Verified Answer
The correct answer is:
$\frac{g}{e}$
The given situation is shown in the following figure
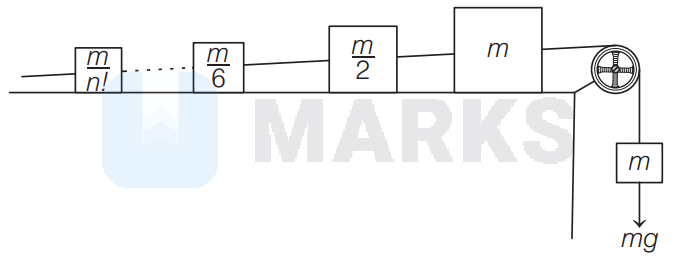
Effective mass of the system of $n$ masses placed on the table,
$M=m+\frac{m}{2}+\frac{m}{6}+\ldots+\frac{m}{n !}$
$=m\left(1+\frac{1}{2}+\frac{1}{6}+\ldots+\frac{1}{n !}\right)$
$=m\left(\frac{1}{1 !}+\frac{1}{2 !}+\frac{1}{3 !}+\ldots+\frac{1}{n !}\right)$
$=m\left(1+\frac{1}{1 !}+\frac{1}{2 !}+\frac{1}{3 !}+\ldots+\frac{1}{n !}-1\right)$
$M=m(e-1)$
$\left[\because e=1+\frac{1}{1 !}+\frac{1}{2 !}+\frac{1}{3 !}+\ldots+\frac{1}{n !}\right]$
The given system of masses can be redrawn as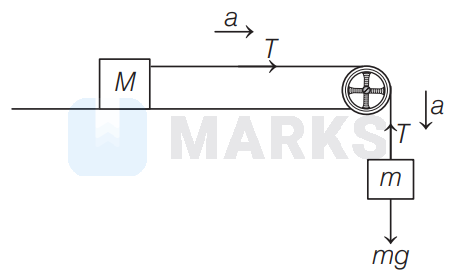
If $a$ be the acceleration of system of masses, then according to Newton's second law of motion,
$T=M a \Rightarrow T=m(e-1) a$ $\ldots(i)$
and $m g-T=m a \Rightarrow T=m g-m a$
$T=m(g-a)$ $\ldots(ii)$
From Eq. (i) and Eq. (ii), we get
$m(e-1) a=m(g-a) \Rightarrow a=g / e$
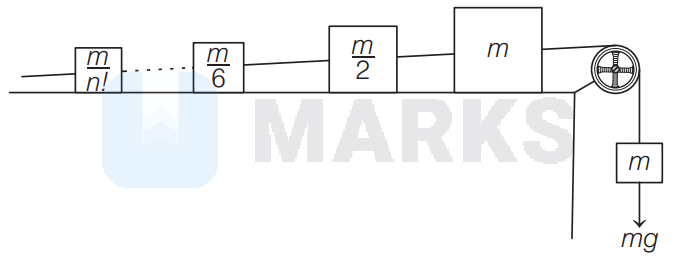
Effective mass of the system of $n$ masses placed on the table,
$M=m+\frac{m}{2}+\frac{m}{6}+\ldots+\frac{m}{n !}$
$=m\left(1+\frac{1}{2}+\frac{1}{6}+\ldots+\frac{1}{n !}\right)$
$=m\left(\frac{1}{1 !}+\frac{1}{2 !}+\frac{1}{3 !}+\ldots+\frac{1}{n !}\right)$
$=m\left(1+\frac{1}{1 !}+\frac{1}{2 !}+\frac{1}{3 !}+\ldots+\frac{1}{n !}-1\right)$
$M=m(e-1)$
$\left[\because e=1+\frac{1}{1 !}+\frac{1}{2 !}+\frac{1}{3 !}+\ldots+\frac{1}{n !}\right]$
The given system of masses can be redrawn as

If $a$ be the acceleration of system of masses, then according to Newton's second law of motion,
$T=M a \Rightarrow T=m(e-1) a$ $\ldots(i)$
and $m g-T=m a \Rightarrow T=m g-m a$
$T=m(g-a)$ $\ldots(ii)$
From Eq. (i) and Eq. (ii), we get
$m(e-1) a=m(g-a) \Rightarrow a=g / e$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.