Search any question & find its solution
Question:
Answered & Verified by Expert
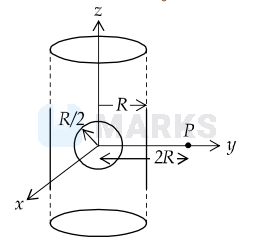
An infinitely long solid cylinder of radius $R$ has a uniform volume charge density $\rho$. It has a spherical cavity of radius $R / 2$ with its centre on the axis of the cylinder, as shown in the figure. The magnitude of the electric field at the point $P$, which is at a distance $2 R$ from the axis of the cylinder, is given by the expression $\frac{23 \rho R}{16 K \varepsilon_{0}}$. The value of $k$ is

Solution:
2164 Upvotes
Verified Answer
The correct answer is:
6
The magnitude of the electric field at the point $P$ which is at a distance $2 R$ from the axis of the cylinder
$\begin{array}{l}
\mathrm{E}=\mathrm{E}_{\text {total }}-\mathrm{E}_{\text {cavity }} \\
=\frac{\gamma}{2 \pi \varepsilon_{0}(2 R)}-\frac{1}{4 \pi \varepsilon_{0}} \frac{Q}{(2 R)^{2}} \\
\mathrm{Q}_{\text {sphere }}=\frac{4}{3} \pi\left(\frac{R}{2}\right)^{3} \rho=\frac{\pi R^{3} \rho}{6} \\
\begin{array}{l}
\lambda_{\text {cylinder }}=\pi R^{2} \rho \\
\therefore E=\frac{\pi R^{2} \rho}{4 \pi \varepsilon_{0} R}-\frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{\pi R^{3} \rho / 6}{4 R^{2}} \\
=\frac{23 \rho R}{96 \varepsilon_{0}}=\frac{23 \rho R}{16 \times 6 \times \varepsilon_{0}} \\
\therefore k=6
\end{array}
\end{array}$
$\begin{array}{l}
\mathrm{E}=\mathrm{E}_{\text {total }}-\mathrm{E}_{\text {cavity }} \\
=\frac{\gamma}{2 \pi \varepsilon_{0}(2 R)}-\frac{1}{4 \pi \varepsilon_{0}} \frac{Q}{(2 R)^{2}} \\
\mathrm{Q}_{\text {sphere }}=\frac{4}{3} \pi\left(\frac{R}{2}\right)^{3} \rho=\frac{\pi R^{3} \rho}{6} \\
\begin{array}{l}
\lambda_{\text {cylinder }}=\pi R^{2} \rho \\
\therefore E=\frac{\pi R^{2} \rho}{4 \pi \varepsilon_{0} R}-\frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{\pi R^{3} \rho / 6}{4 R^{2}} \\
=\frac{23 \rho R}{96 \varepsilon_{0}}=\frac{23 \rho R}{16 \times 6 \times \varepsilon_{0}} \\
\therefore k=6
\end{array}
\end{array}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.