Given arrangement is shown below


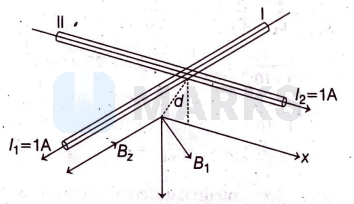
Distance of conductor I from origin, is
$$
\begin{aligned}
& d=\sqrt{x^2+y^2}=\sqrt{1+1} \\
\Rightarrow \quad & d=\sqrt{2} \mathrm{~cm}=\sqrt{2} \times 10^{-2} \mathrm{~m}
\end{aligned}
$$

Magnetic field due to wire Iat origin is
$$
B_1=\frac{\mu_0 I_1}{2 \pi d}
$$
or $\quad B_1=B_0=\frac{\mu_0}{2 \pi d}$
$$
\left[\therefore I_1=I_2=1 \mathrm{~A}\right]
$$

Now, in vector form, $\mathbf{B}_1=\frac{\mu_0}{2 \pi d}\left(\frac{1}{\sqrt{2}} \hat{i}-\frac{1}{\sqrt{2}} \hat{j}\right)$
$$
=\frac{\mu_0}{2 \pi \times \sqrt{2} \times 10^{-2}}\left(\frac{1}{\sqrt{2}} \hat{i}-\frac{1}{\sqrt{2}} \hat{j}\right)
$$

And field of conductor II is
$$
\begin{aligned}
\mathbf{B}_2 & =\frac{\mu_0 I_2}{2 \pi y}(-\hat{k}) \\
& =\frac{\mu_0}{2 \pi \times 10^{-2}}(-\hat{k}) \quad\left[\therefore y=1 \mathrm{~cm}=1 \times 10^{-2} \mathrm{~m}\right]
\end{aligned}
$$

Hence, magnetic field due to both conductors,
$$
\begin{aligned}
& \mathbf{B}=\mathbf{B}_1+\mathbf{B}_2 \\
& =\frac{\mu_0}{2 \pi}\left(\frac{1}{\sqrt{2}} \hat{i}-\frac{1}{\sqrt{2}} \hat{j}\right) \times \frac{1}{\sqrt{2} \times 10^{-2}}+\frac{\mu_0}{2 \pi}(-\hat{k}) \times \frac{1}{10^{-2}} \\
& \Rightarrow \mathbf{B}=\frac{\mu_0}{2 \pi \times 10^{-2}}\left\{\frac{\hat{i}}{2}-\frac{\hat{j}}{2}-\hat{k}\right\}
\end{aligned}
$$

Hence, ratio $\frac{\mathbf{B}}{B_0}$ is
$\begin{aligned} & \frac{\mathbf{B}}{B_0}=\left(\frac{\frac{\mu_0}{2 \pi \times 10^{-2}}\left(\frac{\hat{i}}{2}-\frac{\hat{j}}{2}-\hat{k}\right)}{\frac{\mu_0}{2 \pi \times \sqrt{2} \times 10^{-2}}}\right)=\left(\frac{\hat{i}}{2}-\frac{\hat{j}}{2}-\hat{k}\right) \sqrt{2} \\ & \frac{\hat{i}}{\sqrt{2}}-\frac{\hat{j}}{\sqrt{2}}-\sqrt{2} \hat{k} \\ & \frac{\mathbf{B}}{B_0}=\left(\frac{1}{\sqrt{2}},-\frac{1}{\sqrt{2}},-\sqrt{2}\right)\end{aligned}$