Search any question & find its solution
Question:
Answered & Verified by Expert
An insect crawls up a hemispherical surface very slowly. The coefficient of friction between the insect and the surface is $1 / 3$. If the line joining the centre of the hemispherical surface to the insect makes an angle $\alpha$ with the vertical, the maximum possible value of $\alpha$ so that the insect does not slip is given by
Options:

Solution:
1536 Upvotes
Verified Answer
The correct answer is:
$\cot \alpha=3$
$\cot \alpha=3$
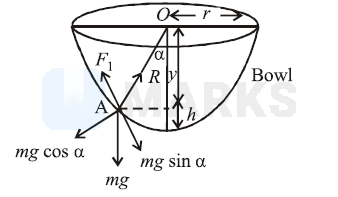
The insect crawls up the bowl upto a certain height $h$ only till the component of its weight along the bowl is balanced by limiting frictional force.
For limiting condition at point $\mathrm{A}$ $R=m g \cos \alpha$
$F_1=m g \sin \alpha$
Dividing eq. (ii) by (i)
$\tan \alpha=\frac{1}{\cot \alpha}=\frac{F_1}{R}=\mu\left[\right.$ As $\left.F_1=\mu R\right]$ $\Rightarrow \quad \tan \alpha=\mu=\frac{1}{3}\left[\because \mu=\frac{1}{3}(\right.$ Given $\left.]\right)$ $\therefore \quad \cot \alpha=3$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.