Search any question & find its solution
Question:
Answered & Verified by Expert
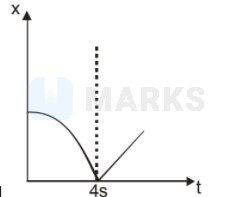
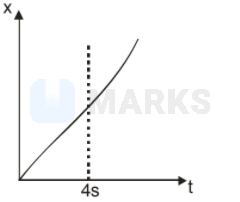
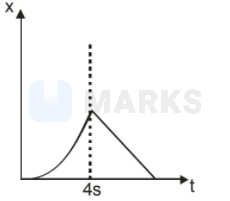
An object at rest at the origin begins to move in the $+x$ direction with a uniform acceleration of $1 \mathrm{~m} / \mathrm{s}^{2}$ for $4 \mathrm{~s}$ and then it continues moving with a uniform velocity of $4 \mathrm{~m} / \mathrm{s}$ in the same direction. The $\mathrm{x}-\mathrm{t}$ graph for object's motion will be
Options:
Solution:
1148 Upvotes
Verified Answer
The correct answer is:
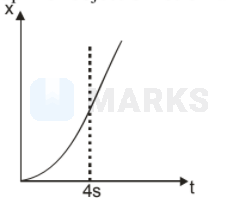

$$
\begin{array}{l}
\mathrm{V}=0+1 \times \mathrm{t} \\
\frac{d x}{d t}=t \\
d x=t \mathrm{dt} \\
x \propto t^{2} \quad \ldots \ldots \ldots \\ Parabolic
\frac{d x}{d t}=4 \\
d x=4 d t \\
x \propto t \quad \ldots \ldots \ldots Linear
\end{array}
$$
\begin{array}{l}
\mathrm{V}=0+1 \times \mathrm{t} \\
\frac{d x}{d t}=t \\
d x=t \mathrm{dt} \\
x \propto t^{2} \quad \ldots \ldots \ldots \\ Parabolic
\frac{d x}{d t}=4 \\
d x=4 d t \\
x \propto t \quad \ldots \ldots \ldots Linear
\end{array}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.