Search any question & find its solution
Question:
Answered & Verified by Expert
An object moves with speed $v_1, v_2$ and $v_3$ along a line segment $A B, B C$ and $C D$ respectively as shown in figure. Where $A B=B C$ and $A D=3 A B$, then average speed of the object will be:

Options:

Solution:
1153 Upvotes
Verified Answer
The correct answer is:
$\frac{3 v_1 v_2 v_3}{\left(v_1 v_2+v_2 v_3+v_3 v_1\right)}$
Consider,
$\mathrm{AB}=x$
$\mathrm{BC}=x$
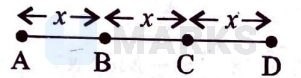
$2 x+\mathrm{CD}=3 x \Rightarrow \mathrm{CD}=3 x-2 x=x$
Average speed of the object $ < \mathrm{v}>$
$=\frac{\text { Total distance }}{\text { Total time }}$
$ < \mathrm{v}>=\frac{3 x}{\frac{x}{v_1}+\frac{x}{v_2}+\frac{x}{v_3}}=\frac{3 v_1 v_2 v_3}{v_2 v_3+v_1 v_3+v_1 v_2}$
$\mathrm{AB}=x$
$\mathrm{BC}=x$

$2 x+\mathrm{CD}=3 x \Rightarrow \mathrm{CD}=3 x-2 x=x$
Average speed of the object $ < \mathrm{v}>$
$=\frac{\text { Total distance }}{\text { Total time }}$
$ < \mathrm{v}>=\frac{3 x}{\frac{x}{v_1}+\frac{x}{v_2}+\frac{x}{v_3}}=\frac{3 v_1 v_2 v_3}{v_2 v_3+v_1 v_3+v_1 v_2}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.