Search any question & find its solution
Question:
Answered & Verified by Expert
An open U-tube contains mercury. When $11.2 \mathrm{~cm}$ of water is poured into one of the arms of the tube, how high does the mercury rise in the other arm from its initial unit?
Options:
Solution:
1879 Upvotes
Verified Answer
The correct answer is:
$0.41 \mathrm{~cm}$
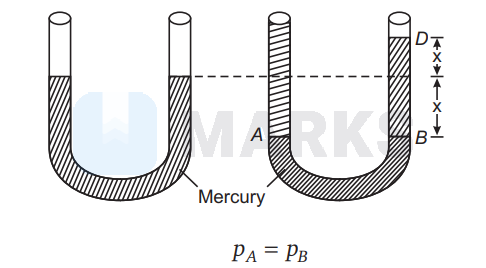
On pouring water on left side, mercury rises $x$ $\mathrm{cm}$ (say) from its previous level in the right limb of U-tube creating a difference of levels of mercury by $2 x \mathrm{~cm} .$ Equating pressure at $A$ and $B$, we get
$$
\begin{array}{l}
\quad p_{A}=p_{B} \\
\therefore 11.2 \times 10^{-2} \times \rho_{\text {water }} \times g=2 x \times \rho_{\mathrm{Hg}} \times g \\
11.2 \times 10^{-2} \times 1000 \mathrm{~kg} / \mathrm{m}^{3} \\
=2 x \times 13600 \mathrm{~kg} / \mathrm{m}^{3} \\
x=\frac{11.2 \times 10^{-2} \times 1000}{2 \times 13600} \mathrm{~m} \\
=0.41 \mathrm{~cm}
\end{array}
$$

$$
\begin{array}{l}
\quad p_{A}=p_{B} \\
\therefore 11.2 \times 10^{-2} \times \rho_{\text {water }} \times g=2 x \times \rho_{\mathrm{Hg}} \times g \\
11.2 \times 10^{-2} \times 1000 \mathrm{~kg} / \mathrm{m}^{3} \\
=2 x \times 13600 \mathrm{~kg} / \mathrm{m}^{3} \\
x=\frac{11.2 \times 10^{-2} \times 1000}{2 \times 13600} \mathrm{~m} \\
=0.41 \mathrm{~cm}
\end{array}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.