The given curve is
$\begin{array}{l}
\pi\left[4(x-\sqrt{2})^{2}+y^{2}\right]=8 \\
4(x-\sqrt{2})^{2}+y^{2}=\frac{8}{\pi} \\
(x-\sqrt{2})^{2}+\left(\frac{y}{2}\right)^{2}=\frac{2}{\pi} \\
\frac{(x-\sqrt{2})^{2}}{\left(\sqrt{\frac{2}{\pi}}\right)^{2}}+\frac{y^{2}}{\left(2 \sqrt{\frac{2}{\pi}}\right)^{2}}=1 ...(1)
\end{array}$
This is the equation of the ellipse having centre $(\sqrt{2}, 0)$
Observe the figure of ellipse (1). The centre
Pis $(\sqrt{2}, 0)$. A and B are $\left(\sqrt{2},-\sqrt{\frac{2}{\pi}}, 0\right)$ and $\left(\sqrt{2}+\sqrt{\frac{2}{\pi}}, 0\right)$ respectively.


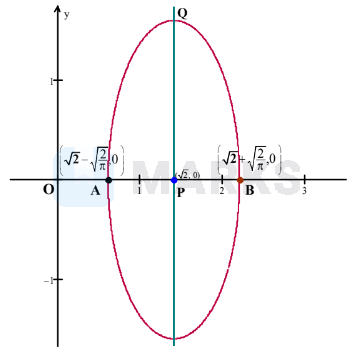
The required area $=4 \times$ area of figure $\mathrm{PQB}$
$\begin{array}{l}
=4 \times \int_{\sqrt{2}}^{\sqrt{2}+\sqrt{\frac{2}{\pi}}} y d x \\
=4 \times \int_{\sqrt{2}}^{\sqrt{2}+\sqrt{\frac{2}{\pi}}} \sqrt{\frac{8}{\pi}-4(x-\sqrt{2})^{2}} d x \\
=4 \times 2 \int_{\sqrt{2}}^{\sqrt{2}+\sqrt{\frac{2}{\pi}}} \sqrt{\left(\sqrt{\frac{2}{\pi}}\right)^{2}-(x-\sqrt{2})^{2}} d x \\
=8\left[\frac{x-\sqrt{2}}{2} \sqrt{\frac{2}{\pi}-(x-\sqrt{2})^{2}}+\right. \left.\frac{(2 / \pi)}{2} \sin ^{-1}\left(\frac{x-\sqrt{2}}{\sqrt{2 / \pi}}\right)\right]_{\sqrt{2}}^{\sqrt{2}+\sqrt{\frac{2}{\pi}}}
\end{array}$
$\left[\because \int \sqrt{\mathrm{a}^{2}-\mathrm{x}^{2}} \mathrm{dx}=\frac{1}{2} \mathrm{x} \sqrt{\mathrm{a}^{2}-\mathrm{x}^{2}}+\frac{\mathrm{a}^{2}}{2} \sin ^{-1} \frac{\mathrm{x}}{\mathrm{a}}+\mathrm{C}\right]$
$=8\left[\left\{\frac{\sqrt{2}+\sqrt{\frac{2}{\pi}}-\sqrt{2}}{2} \sqrt{\frac{2}{\pi}-\left(\sqrt{2}+\sqrt{\frac{2}{\mathrm{x}}}-\sqrt{2}\right)^{2}}\right.\right.$
$\left.+\frac{1}{\pi} \sin ^{-1}\left(\frac{\sqrt{2}+\sqrt{\frac{2}{\pi}}-\sqrt{2}}{\sqrt{\frac{2}{\pi}}}\right)\right\}-\left\{\frac{\sqrt{2}-\sqrt{2}}{2}\right.$
$\left.\left.\sqrt{\frac{2}{\pi}-(\sqrt{2}-\sqrt{2})^{2}}+\frac{1}{\pi} \sin ^{-1}\left(\frac{\sqrt{2}-\sqrt{2}}{\sqrt{2 / \pi}}\right)\right\}\right]$
$=8\left[\frac{1}{\sqrt{2 \pi}}(0)+\frac{1}{\pi} \sin ^{-1}(1)-0-0\right]$
$=8\left(\frac{1}{\pi} \times \frac{\pi}{2}\right)=4$ square units.