Search any question & find its solution
Question:
Answered & Verified by Expert
Area lying between the curves \( y^{2}=2 x \) and \( y=x \)
Options:
Solution:
2498 Upvotes
Verified Answer
The correct answer is:
\( \frac{2}{3} \) sq. units
Given curves,
$$
\begin{array}{l}
y^{2}=2 x \rightarrow(1) \\
y=x \rightarrow(2)
\end{array}
$$
At $x=0$ and $x=2$ we have two intersect points, that is, $(0,0),(2,2)$.
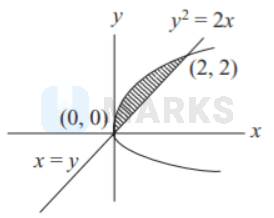
Therefore, required area is given by
$$
\begin{array}{l}
\int_{0}^{2}(\sqrt{2} \sqrt{x}-x) d x \\
=\left[\sqrt{2}\left(\frac{2}{3} x^{3 / 2}\right)-\frac{x^{2}}{2}\right]^{2} \\
=\left(\frac{2 \sqrt{2}}{3}\left(2^{3 / 2}\right)-\frac{4}{2}\right) \\
=\frac{2}{3} \cdot 2^{2}-2=\frac{2}{3} \text { sq. units }
\end{array}
$$
$$
\begin{array}{l}
y^{2}=2 x \rightarrow(1) \\
y=x \rightarrow(2)
\end{array}
$$
At $x=0$ and $x=2$ we have two intersect points, that is, $(0,0),(2,2)$.

Therefore, required area is given by
$$
\begin{array}{l}
\int_{0}^{2}(\sqrt{2} \sqrt{x}-x) d x \\
=\left[\sqrt{2}\left(\frac{2}{3} x^{3 / 2}\right)-\frac{x^{2}}{2}\right]^{2} \\
=\left(\frac{2 \sqrt{2}}{3}\left(2^{3 / 2}\right)-\frac{4}{2}\right) \\
=\frac{2}{3} \cdot 2^{2}-2=\frac{2}{3} \text { sq. units }
\end{array}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.