Search any question & find its solution
Question:
Answered & Verified by Expert
Area of the region (in square units) bounded by the curve $y=x^2+4$ and the line $y=5 x-2$ is
Options:
Solution:
2892 Upvotes
Verified Answer
The correct answer is:
$\frac{1}{6}$
We have,
$$
y=x^2+4, y=5 x-2
$$
Solving equation, we get
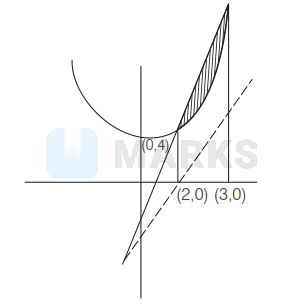
$(2,8)$ and $(3,13)$
Area of shaded region
$$
\begin{aligned}
& \int_2^3\left((5 x-2)-\left(x^2+4\right) d x\right. \\
& =\int_2^3\left(5 x-x^2-6\right) d x=\left[\frac{5 x^2}{2}-\frac{x^3}{3}-6 x\right]_2^3 \\
& =\left[\left(\frac{45}{2}-9-18\right)-\left(10-\frac{8}{3}-12\right)\right]=\frac{1}{6}
\end{aligned}
$$
$$
y=x^2+4, y=5 x-2
$$
Solving equation, we get

$(2,8)$ and $(3,13)$
Area of shaded region
$$
\begin{aligned}
& \int_2^3\left((5 x-2)-\left(x^2+4\right) d x\right. \\
& =\int_2^3\left(5 x-x^2-6\right) d x=\left[\frac{5 x^2}{2}-\frac{x^3}{3}-6 x\right]_2^3 \\
& =\left[\left(\frac{45}{2}-9-18\right)-\left(10-\frac{8}{3}-12\right)\right]=\frac{1}{6}
\end{aligned}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.