Search any question & find its solution
Question:
Answered & Verified by Expert
As shown in fig. when a spherical cavity (centred at $O$ ) of radius 1 is cut out of a uniform sphere of radius $R$ (centred at $C$ ), the centre of mass of remaining (shaded) part of sphere is at $G$, i.e on the surface of the cavity. $R$ can be determined by the equation :
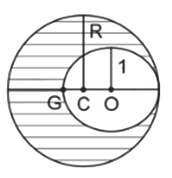
Options:

Solution:
2088 Upvotes
Verified Answer
The correct answer is:
$\left(R^2+R+1\right)(2-R)=1$
Option $3:\left(R^2+R+1\right)(2-R)=1$
CONCEPT:
Centre of mass (COM):
- Centre of mass of a body is a physical point that can be imagined to hold all of the mass of the body.
- In other words, the point along which if any external force is applied there will be only be transitional motion of the body and no rotational motion.
Mathematically, $x_{c m}=\sum m_i x_i / \sum m_i$ and $Y_{c m}=\sum m_i y_i / \sum m_i$
where, $\mathrm{m}_{\mathrm{i}}=$ mass of the ith particle, $\mathrm{x}_{\mathrm{i}}$ and $\mathrm{y}_{\mathrm{i}}$ are the $\mathrm{x}$ and $\mathrm{y}$ coordinates of the body.
EXPLANATION:
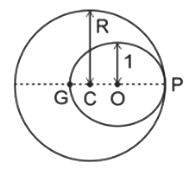
The center of the sphere is at $\mathrm{C}$ and the center of the cavity is at $\mathrm{O}$.
We use the superposition principle to solve the problem.
The sphere with a spherical cavity can be imagined as the sum of the sphere with a positive mass and a smaller sphere with a negative mass.
Let's take the mass density of the sphere as $+\rho$
and take the mass density of the cavity as - $\rho$
So, the mass of the sphere $m_1=$ volume $\times$ density $=(4 / 3) \pi R^3 \rho$ and the mass of the cavity $m_2=$ volume $\times$ density $=(4 / 3) \pi(1)^3(-\rho)=-(4 / 3) \pi \rho$
(where $\rho$ is the density of the material)
We take $C$ as origin $(x, y=0,0)$
The center of mass of the sphere is at $C(0,0)$.
From the figure $C O=C P-O P=R-1$
The center of mass of the cavity is at $O(R-1,0)$
Centre of mass of the whole system (sphere + cavity)
$\mathrm{X}_{\mathrm{cm}}=\frac{0 \times m_1+(R-1) \times m_2}{m_1+m_2}=\frac{(R-1) \times \frac{4}{3} \pi(1)^3(-\rho)}{\frac{4}{3} \pi R^3 \rho+\frac{4}{3} \pi(1)^3(-\rho)}=-\frac{(R-1)}{R^3-1}$
Again, $G C=G O \cdot C O=1 \cdot(R-1)=2 \cdot R$
according to the question centre of mass is at $G$ i.e. at ( $2-R, 0)$
$\Rightarrow X_{c m}=2 \cdot R$
$\begin{aligned} & \Rightarrow \frac{(R-1)}{R^3-1}=2-R \\ & \Rightarrow \frac{(R-1)}{(R-1)\left(R^2+R+1\right)}=2-R \\ & \Rightarrow \frac{1}{\left(R^2+R+1\right)}=2-R \\ & \Rightarrow\left(R^2+R+1\right)(2-R)=1\end{aligned}$
$R$ can be determined by the above equation.
CONCEPT:
Centre of mass (COM):
- Centre of mass of a body is a physical point that can be imagined to hold all of the mass of the body.
- In other words, the point along which if any external force is applied there will be only be transitional motion of the body and no rotational motion.
Mathematically, $x_{c m}=\sum m_i x_i / \sum m_i$ and $Y_{c m}=\sum m_i y_i / \sum m_i$
where, $\mathrm{m}_{\mathrm{i}}=$ mass of the ith particle, $\mathrm{x}_{\mathrm{i}}$ and $\mathrm{y}_{\mathrm{i}}$ are the $\mathrm{x}$ and $\mathrm{y}$ coordinates of the body.
EXPLANATION:

The center of the sphere is at $\mathrm{C}$ and the center of the cavity is at $\mathrm{O}$.
We use the superposition principle to solve the problem.
The sphere with a spherical cavity can be imagined as the sum of the sphere with a positive mass and a smaller sphere with a negative mass.
Let's take the mass density of the sphere as $+\rho$
and take the mass density of the cavity as - $\rho$
So, the mass of the sphere $m_1=$ volume $\times$ density $=(4 / 3) \pi R^3 \rho$ and the mass of the cavity $m_2=$ volume $\times$ density $=(4 / 3) \pi(1)^3(-\rho)=-(4 / 3) \pi \rho$
(where $\rho$ is the density of the material)
We take $C$ as origin $(x, y=0,0)$
The center of mass of the sphere is at $C(0,0)$.
From the figure $C O=C P-O P=R-1$
The center of mass of the cavity is at $O(R-1,0)$
Centre of mass of the whole system (sphere + cavity)
$\mathrm{X}_{\mathrm{cm}}=\frac{0 \times m_1+(R-1) \times m_2}{m_1+m_2}=\frac{(R-1) \times \frac{4}{3} \pi(1)^3(-\rho)}{\frac{4}{3} \pi R^3 \rho+\frac{4}{3} \pi(1)^3(-\rho)}=-\frac{(R-1)}{R^3-1}$
Again, $G C=G O \cdot C O=1 \cdot(R-1)=2 \cdot R$
according to the question centre of mass is at $G$ i.e. at ( $2-R, 0)$
$\Rightarrow X_{c m}=2 \cdot R$
$\begin{aligned} & \Rightarrow \frac{(R-1)}{R^3-1}=2-R \\ & \Rightarrow \frac{(R-1)}{(R-1)\left(R^2+R+1\right)}=2-R \\ & \Rightarrow \frac{1}{\left(R^2+R+1\right)}=2-R \\ & \Rightarrow\left(R^2+R+1\right)(2-R)=1\end{aligned}$
$R$ can be determined by the above equation.
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.