Search any question & find its solution
Question:
Answered & Verified by Expert
Assertion : $\cot \mathrm{h} x=\frac{1-k}{1+k}(0 < k < 2)$.
Reason : The graph of y = tan h x always lies between the
lines y = –1 and y = 1.
The correct option among the following is
Options:
Reason : The graph of y = tan h x always lies between the
lines y = –1 and y = 1.
The correct option among the following is
Solution:
1558 Upvotes
Verified Answer
The correct answer is:
(A) is false but (R) is true
Assertion : $\operatorname{coth} \mathrm{x}=\frac{1-\mathrm{k}}{1+\mathrm{k}}$
$$
\Rightarrow \frac{\mathrm{e}^{\mathrm{x}}+\mathrm{e}^{-\mathrm{x}}}{\mathrm{e}^{\mathrm{x}}-\mathrm{e}^{-\mathrm{x}}}=\frac{1-\mathrm{k}}{1+\mathrm{k}}
$$
By C \& D
$\Rightarrow \frac{\mathrm{e}^{\mathrm{x}}}{\mathrm{e}^{-\mathrm{x}}}=\frac{-1}{\mathrm{k}} \Rightarrow \mathrm{e}^{2 \mathrm{x}}=-\frac{1}{\mathrm{k}}$ is possible
because $\mathrm{e}^{2 \mathrm{x}}>0, \forall \mathrm{x} \in \mathrm{R}$
But $-\frac{1}{\mathrm{k}} < 0(\because 0 < \mathrm{K} < 2)$
So, assertion is wrong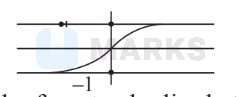
Reason :
It is clear from graph the graph of $y=\tan h x$ lies between $y=-1$ and $y=1$
so, reason is correct.
$$
\Rightarrow \frac{\mathrm{e}^{\mathrm{x}}+\mathrm{e}^{-\mathrm{x}}}{\mathrm{e}^{\mathrm{x}}-\mathrm{e}^{-\mathrm{x}}}=\frac{1-\mathrm{k}}{1+\mathrm{k}}
$$
By C \& D
$\Rightarrow \frac{\mathrm{e}^{\mathrm{x}}}{\mathrm{e}^{-\mathrm{x}}}=\frac{-1}{\mathrm{k}} \Rightarrow \mathrm{e}^{2 \mathrm{x}}=-\frac{1}{\mathrm{k}}$ is possible
because $\mathrm{e}^{2 \mathrm{x}}>0, \forall \mathrm{x} \in \mathrm{R}$
But $-\frac{1}{\mathrm{k}} < 0(\because 0 < \mathrm{K} < 2)$
So, assertion is wrong

Reason :
It is clear from graph the graph of $y=\tan h x$ lies between $y=-1$ and $y=1$
so, reason is correct.
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.