Search any question & find its solution
Question:
Answered & Verified by Expert
Assuming the atom is in the ground state, the expression for the magnetic field at a point nucleus in hydrogen atom due to circular motion of electron is
$\left[\begin{array}{l}\mu_0 \rightarrow \text { permeability of free space, } m \rightarrow \text { mass of electron } \\ \varepsilon_0 \rightarrow \text { permittivity of free space, } h \rightarrow \text { Planck's constant }\end{array}\right]$
Options:
$\left[\begin{array}{l}\mu_0 \rightarrow \text { permeability of free space, } m \rightarrow \text { mass of electron } \\ \varepsilon_0 \rightarrow \text { permittivity of free space, } h \rightarrow \text { Planck's constant }\end{array}\right]$
Solution:
1506 Upvotes
Verified Answer
The correct answer is:
$\frac{\mu_0 e^7 \pi m^2}{8 \varepsilon_0^3 h^5}$
To keep the electron in its orbit, the centripetal force on the electron must be equal to the electrostatic force of attraction,
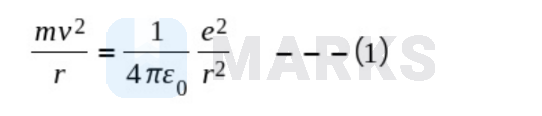
According to Bohr's angular momentum quantization condition:
$\Rightarrow \pi r m e^2=\varepsilon_0 h^2$
$r=\frac{\varepsilon_0 h^2}{\pi m e^2} \quad---(3)$
From (ii) and (iii), we have
$v=\frac{h \pi m e^2}{2 \pi m \varepsilon_0 h^2}=\frac{e^2}{2 \varepsilon_0 h}$
The magnetic field at the center of the circular loop is given by,
$B=\frac{\mu_0 I}{2 r}$
where, current $I=\frac{\mathrm{q}}{\mathrm{T}}$ and time $T=\frac{2 \pi r}{v}$
$\therefore I=\frac{e v}{2 \pi r}$

Using, equations (2), (3) and (4) we have,
$B=\frac{\mu_0 e^7 \pi m^2}{8 \varepsilon_0^3 h^5}$
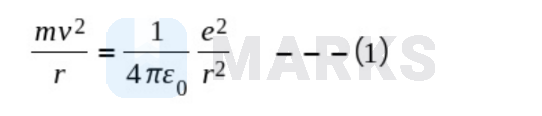
According to Bohr's angular momentum quantization condition:
$\Rightarrow \pi r m e^2=\varepsilon_0 h^2$
$r=\frac{\varepsilon_0 h^2}{\pi m e^2} \quad---(3)$
From (ii) and (iii), we have
$v=\frac{h \pi m e^2}{2 \pi m \varepsilon_0 h^2}=\frac{e^2}{2 \varepsilon_0 h}$
The magnetic field at the center of the circular loop is given by,
$B=\frac{\mu_0 I}{2 r}$
where, current $I=\frac{\mathrm{q}}{\mathrm{T}}$ and time $T=\frac{2 \pi r}{v}$
$\therefore I=\frac{e v}{2 \pi r}$

Using, equations (2), (3) and (4) we have,
$B=\frac{\mu_0 e^7 \pi m^2}{8 \varepsilon_0^3 h^5}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.