Search any question & find its solution
Question:
Answered & Verified by Expert
At a temperature of $314 \mathrm{~K}$ and a pressure of $100 \mathrm{kPa}$, the speed of sound in a gas is $1380 \mathrm{~ms}^{-1}$. The radius of each gas molecule is $0.5 Å$. The frequency of sound at which the wavelength of sound wave in the gas becomes equal to the mean free path of the gas molecules is $\left(\right.$ Boltzmann constant $=1.38 \times 10^{-23} \mathrm{JK}^{-1}$.)
Options:
Solution:
1051 Upvotes
Verified Answer
The correct answer is:
$1000 \sqrt{2} \mathrm{MHz}$
Given, temperature, $T=314 \mathrm{~K}$, pressure, $p=100 \mathrm{kPa},=1.0 \times 10^5 \mathrm{~Pa}$, speed of sound, $v=1380 \mathrm{~ms}^{-1}$ and diameter of gas molecule, $d=10^{-10} \mathrm{~m}$ or radius $r=\frac{1}{2} \times 10^{-10} \mathrm{~m}=\frac{1}{2} Å$
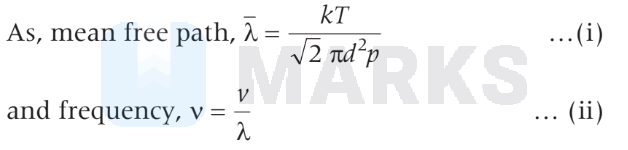
So, from Eqs. (i) and (ii), we get
$$
v=\frac{\sqrt{2} \pi d^2 p \times v}{k T}
$$
Now, putting the given values, we get
$$
\begin{aligned}
& =\frac{\sqrt{2} \times 3.14 \times 10^{-20} \times 10^5 \times 1380}{1.38 \times 10^{-23} \times 314} \\
v & =\sqrt{2} \times 10^9 \mathrm{~Hz} \Rightarrow v=1000 \sqrt{2} \mathrm{MHz}
\end{aligned}
$$
Hence, the correct option is (b).
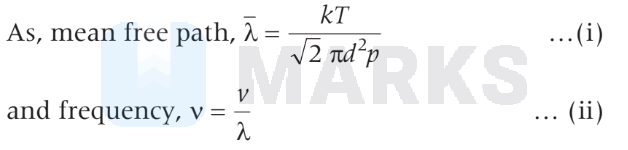
So, from Eqs. (i) and (ii), we get
$$
v=\frac{\sqrt{2} \pi d^2 p \times v}{k T}
$$
Now, putting the given values, we get
$$
\begin{aligned}
& =\frac{\sqrt{2} \times 3.14 \times 10^{-20} \times 10^5 \times 1380}{1.38 \times 10^{-23} \times 314} \\
v & =\sqrt{2} \times 10^9 \mathrm{~Hz} \Rightarrow v=1000 \sqrt{2} \mathrm{MHz}
\end{aligned}
$$
Hence, the correct option is (b).
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.