Search any question & find its solution
Question:
Answered & Verified by Expert
At time $t=0$, a force $\mathrm{F}=\alpha t$, where $t$ is time in seconds, is applied to a body of mass $1 \mathrm{~kg}$, resting on a smooth horizontal plane. If the direction of the force makes an angle of $45^{\circ}$ with the horizontal, then the velocity of the body at the moment of its breaking off the plane is
Options:
Solution:
1421 Upvotes
Verified Answer
The correct answer is:
$\frac{50 \sqrt{2}}{\alpha} \mathrm{m} / \mathrm{s}$
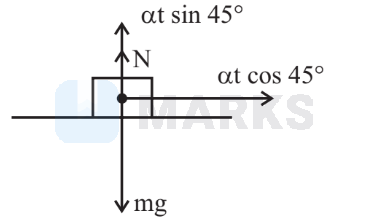
Let at $\mathrm{t}=\mathrm{t}_0$, body leaves the plate Then, at $\mathrm{t}=\mathrm{t}_0 \stackrel{\mathrm{N}}{\Rightarrow}=0$ and $\mathrm{V}=\mathrm{V}_{\text {max }}$ So, $\Delta_{\mathrm{O}}+\alpha \mathrm{t}_0 \sin 45^{\circ}=\mathrm{mg}$
$$
\Rightarrow \quad t_0=\frac{m g}{\alpha \sin 45^{\circ}}=\frac{10 \sqrt{2}}{\alpha}
$$
Now, $a=\frac{d V}{d t}$
$$
\begin{aligned}
& \int_0^{\mathrm{dV}=\mathrm{adt}} \mathrm{dV}=\alpha \cos 45^{\circ} \int_0^{\mathrm{t}_0} \mathrm{tdt} \quad\left[\because \mathrm{a}=\frac{\alpha \mathrm{t} \cos 45^{\circ}}{\mathrm{m}}\right] \\
& \mathrm{V}_{\max }=\frac{\alpha \mathrm{t}_0^2}{2 \sqrt{2}}=\frac{\alpha}{2 \sqrt{2}} \times \frac{200}{\alpha^2}=\frac{50 \sqrt{2}}{\alpha}
\end{aligned}
$$
$$
\Rightarrow \quad t_0=\frac{m g}{\alpha \sin 45^{\circ}}=\frac{10 \sqrt{2}}{\alpha}
$$

Now, $a=\frac{d V}{d t}$
$$
\begin{aligned}
& \int_0^{\mathrm{dV}=\mathrm{adt}} \mathrm{dV}=\alpha \cos 45^{\circ} \int_0^{\mathrm{t}_0} \mathrm{tdt} \quad\left[\because \mathrm{a}=\frac{\alpha \mathrm{t} \cos 45^{\circ}}{\mathrm{m}}\right] \\
& \mathrm{V}_{\max }=\frac{\alpha \mathrm{t}_0^2}{2 \sqrt{2}}=\frac{\alpha}{2 \sqrt{2}} \times \frac{200}{\alpha^2}=\frac{50 \sqrt{2}}{\alpha}
\end{aligned}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.