Search any question & find its solution
Question:
Answered & Verified by Expert
Back surface of a glass (refractive index $\mathrm{n}$ and thickness $\mathrm{t}$ ) is polished to work as a mirror as shown below. A laser beam falls on it and is partially reflected and refracted at the air-glass interface and fully reflected at the mirror surface respectively. A pattern of discrete spots of light is observed on the screen.
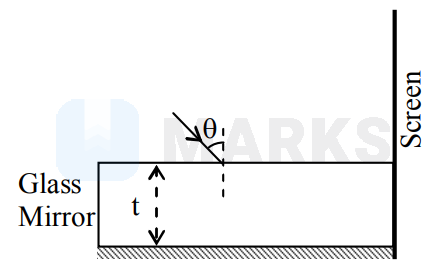
The spacing between the spots on the screen will be
Options:

The spacing between the spots on the screen will be
Solution:
1049 Upvotes
Verified Answer
The correct answer is:
$\frac{2 t \cos \theta}{\sqrt{n^{2}-\sin ^{2} \theta}}$
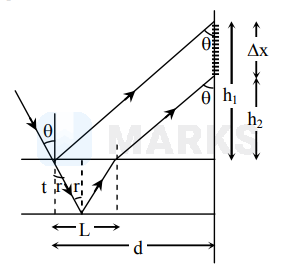
Therefore $\Delta \mathrm{x}=\mathrm{h}_{1}-\mathrm{h}_{2}$
$$
\begin{array}{l}
\tan \theta=\frac{\mathrm{d}}{\mathrm{h}_{1}} \& \tan \theta=\frac{\mathrm{d}-\mathrm{L}}{\mathrm{h}_{2}} \\
\Delta \mathrm{x}=\frac{\mathrm{d}}{\tan \theta}-\frac{\mathrm{d}-\mathrm{L}}{\tan \theta} \\
\Delta \mathrm{x}=\frac{\mathrm{L}}{\tan \theta}
\end{array}
$$
Snell's Law
$$
\begin{array}{l}
1 \cdot \sin \theta=\mathrm{n} \cdot \sin \mathrm{r} \Rightarrow 1 \sin \mathrm{r}=\frac{\sin \theta}{\mathrm{n}} \\
\tan \mathrm{r}=\frac{\mathrm{L}}{2 . \mathrm{t}} \Rightarrow \mathrm{L}=2 \mathrm{t} \tan \mathrm{r}
\end{array}
$$
$$
\mathrm{L}=\frac{2 \mathrm{t} \cdot \sin \theta}{\sqrt{\mathrm{n}^{2}-\sin ^{2} \theta}}
$$
$$
\begin{array}{l}
\therefore \Delta \mathrm{x}=\frac{2 \mathrm{t} \sin \theta}{\sqrt{\mathrm{n}^{2}-\sin ^{2} \theta} \tan \theta} \\
\tan \theta=\frac{2 \mathrm{t} \cos \theta}{\sqrt{\mathrm{n}^{2}-\sin ^{2} \theta}}
\end{array}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.