Search any question & find its solution
Question:
Answered & Verified by Expert
Calculate the amount of hydrogen gas required in order to produce $100 \mathrm{~g}$ of ammonia by the reaction of $\mathrm{N}_2(g)$ and $\mathrm{H}_2(g)$ gases.
Options:
Solution:
2146 Upvotes
Verified Answer
The correct answer is:
$17.65 \mathrm{~g}$
Ammonia is produced from gaseous $\mathrm{N}_2$ and $\mathrm{H}_2$,
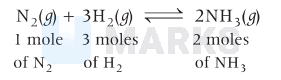
or,
$\begin{array}{lll}28 \mathrm{~g} & 6 \mathrm{~g} & 34 \mathrm{~g}\end{array}$
So, according to above equation,
$\begin{aligned} & 34 \mathrm{~g} \text { of } \mathrm{NH}_3 \text { requires }=6 \mathrm{~g} \text { of } \mathrm{H}_2 \\ & 1 \mathrm{~g} \text { of } \mathrm{NH}_3 \text { requires }=\frac{6}{34} \mathrm{~g} \text { of } \mathrm{H}_2 \\ & 100 \mathrm{~g} \text { of } \mathrm{NH}_3 \text { requires }=\frac{6}{34} \times 100\end{aligned}$
$=17.647 \approx 17.65 \mathrm{~g}$.
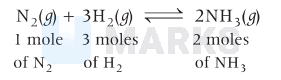
or,
$\begin{array}{lll}28 \mathrm{~g} & 6 \mathrm{~g} & 34 \mathrm{~g}\end{array}$
So, according to above equation,
$\begin{aligned} & 34 \mathrm{~g} \text { of } \mathrm{NH}_3 \text { requires }=6 \mathrm{~g} \text { of } \mathrm{H}_2 \\ & 1 \mathrm{~g} \text { of } \mathrm{NH}_3 \text { requires }=\frac{6}{34} \mathrm{~g} \text { of } \mathrm{H}_2 \\ & 100 \mathrm{~g} \text { of } \mathrm{NH}_3 \text { requires }=\frac{6}{34} \times 100\end{aligned}$
$=17.647 \approx 17.65 \mathrm{~g}$.
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.