Search any question & find its solution
Question:
Answered & Verified by Expert
Calculate the depression in the freezing point of water when \(10 \mathrm{~g}\) of \(\mathrm{CH}_3 \mathrm{CH}_2 \mathrm{CHClCOOH}\) is added to \(250 \mathrm{~g}\) of water. \(\mathrm{K}_{\mathrm{a}}=1.4 \times 10^{-3} \mathrm{~K}_{\mathrm{f}}=\mathbf{1 . 8 6} \mathrm{K} \mathrm{kg} \mathrm{mol}^{-1}\).
Solution:
2151 Upvotes
Verified Answer
Molar mass of \(\mathrm{CH}_3 \mathrm{CH}_2 \mathrm{CHClCOOH}\) \(=122 \cdot 5 \mathrm{~g} \mathrm{~mol}^{-1}\)
No. of moles of \(\mathrm{CH}_3 \mathrm{CH}_2 \mathrm{CHClCOOH}\) present \(=\frac{10}{122 \cdot 5}\) \(=8.16 \times 10^{-2}\) mole.
Molality \(=\frac{8.16 \times 10^{-2}}{250} \times 1000=0.3264 \mathrm{~m}\)
Let \(a\) be the degree of dissociation of \(\mathrm{CH}_3 \mathrm{CH}_2\) \(\mathrm{CHClCOOH}\), then and \(\mathrm{C}\) be the initial concentration of \(\mathrm{CH}_3 \mathrm{CH}_2 \mathrm{CHClCOOH}\)
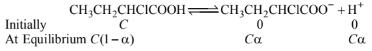
\(\therefore K_a=\frac{C^2 \alpha^2}{C(1-\alpha)}=\frac{C \alpha^2}{1-\alpha}=C \alpha^2\)
\(\{\alpha\) being very very small \(\}\)
\(\begin{aligned}
\therefore K_a &=C \alpha^2 \\
\alpha &=\sqrt{\frac{K_a}{C}}=\sqrt{\frac{1.4 \times 10^{-3}}{0.3264}}=0.065 .
\end{aligned}\)
Calculation of van't Hoff factor: Initially the concentration \(\mathrm{CH}_3 \mathrm{CH}_2 \mathrm{CHClCOOH}\) will be 1 mole.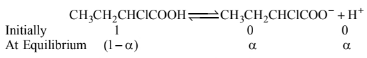
Total moles at equilibrium \(=1-\alpha+\alpha+\alpha=1+\alpha\)
\(\begin{aligned}
&\therefore \quad i=\frac{1+\alpha}{1}=1+\alpha=1+0.065=1.065 \\
&\therefore \quad \Delta T_f=i K_f m=1.065 \times 1.86 \times 0.3264=0.65 \mathrm{~K}
\end{aligned}\)
No. of moles of \(\mathrm{CH}_3 \mathrm{CH}_2 \mathrm{CHClCOOH}\) present \(=\frac{10}{122 \cdot 5}\) \(=8.16 \times 10^{-2}\) mole.
Molality \(=\frac{8.16 \times 10^{-2}}{250} \times 1000=0.3264 \mathrm{~m}\)
Let \(a\) be the degree of dissociation of \(\mathrm{CH}_3 \mathrm{CH}_2\) \(\mathrm{CHClCOOH}\), then and \(\mathrm{C}\) be the initial concentration of \(\mathrm{CH}_3 \mathrm{CH}_2 \mathrm{CHClCOOH}\)
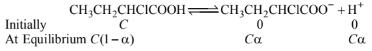
\(\therefore K_a=\frac{C^2 \alpha^2}{C(1-\alpha)}=\frac{C \alpha^2}{1-\alpha}=C \alpha^2\)
\(\{\alpha\) being very very small \(\}\)
\(\begin{aligned}
\therefore K_a &=C \alpha^2 \\
\alpha &=\sqrt{\frac{K_a}{C}}=\sqrt{\frac{1.4 \times 10^{-3}}{0.3264}}=0.065 .
\end{aligned}\)
Calculation of van't Hoff factor: Initially the concentration \(\mathrm{CH}_3 \mathrm{CH}_2 \mathrm{CHClCOOH}\) will be 1 mole.
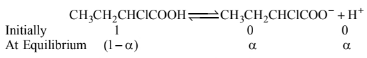
Total moles at equilibrium \(=1-\alpha+\alpha+\alpha=1+\alpha\)
\(\begin{aligned}
&\therefore \quad i=\frac{1+\alpha}{1}=1+\alpha=1+0.065=1.065 \\
&\therefore \quad \Delta T_f=i K_f m=1.065 \times 1.86 \times 0.3264=0.65 \mathrm{~K}
\end{aligned}\)
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.