Search any question & find its solution
Question:
Answered & Verified by Expert
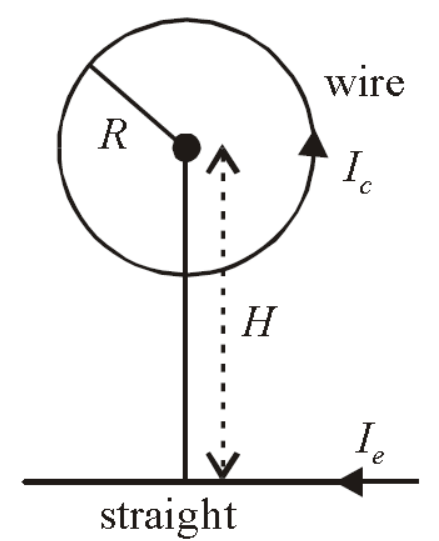
Circular loop of a wire and a long straight wire carry currents $I_c$ and $I_e$ respectively as shown in figure. Assuming that these are placed in the same plane, the magnetic field will be zero at the centre of the loop when separation $H$ is
Options:

Solution:
1738 Upvotes
Verified Answer
The correct answer is:
$\frac{I_e R}{I_c \pi}$
Magnetic field due to a circular loop at the centre of the loop is $B_1=\frac{\mu_0}{4 \pi} \frac{2 \pi I_c}{R}$. Magnetic field due to a straight line at the centre of the loop is $B_2=\frac{\mu_0 2 I_e}{4 \pi H}$
Both these fields act in opposite direction hence total magnetic field at the centre of the loop is
$$
\begin{aligned}
& B=B_1-B_2=\frac{\mu_0 2 \pi I_c}{4 \pi R}-\frac{\mu_0 2 I_e}{4 \pi H} \\
& B=0 \text { (given). } \\
& \therefore \frac{\mu_0 2 \pi I_c}{4 \pi R}=\frac{\mu_0 2 I_e}{4 \pi H} \text { or, } H=\frac{I_e R}{\pi I_c} .
\end{aligned}
$$
Both these fields act in opposite direction hence total magnetic field at the centre of the loop is
$$
\begin{aligned}
& B=B_1-B_2=\frac{\mu_0 2 \pi I_c}{4 \pi R}-\frac{\mu_0 2 I_e}{4 \pi H} \\
& B=0 \text { (given). } \\
& \therefore \frac{\mu_0 2 \pi I_c}{4 \pi R}=\frac{\mu_0 2 I_e}{4 \pi H} \text { or, } H=\frac{I_e R}{\pi I_c} .
\end{aligned}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.