Search any question & find its solution
Question:
Answered & Verified by Expert
Consider one mole of perfect gas in a cylinder of unit crosssection with a piston attached (figure).
A spring (spring constant $k$ )is attached (unstretched length $L$ ) to the piston and to the bottom of the cylinder. Initially the spring is unstretched and the gas is in equilibrium. A certain amount of heat $Q$ is supplied to the gas causing an increase of value from $V_0$ to $\mathrm{V}_1$.
(a) What is the initial pressure of the system?
(b) What is the final pressure of the system?
(c) Using the first law of thermodynamics, write down a relation between $Q, p_{\mathrm{a}}, V, V_0$ and $k$.
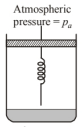
A spring (spring constant $k$ )is attached (unstretched length $L$ ) to the piston and to the bottom of the cylinder. Initially the spring is unstretched and the gas is in equilibrium. A certain amount of heat $Q$ is supplied to the gas causing an increase of value from $V_0$ to $\mathrm{V}_1$.
(a) What is the initial pressure of the system?
(b) What is the final pressure of the system?
(c) Using the first law of thermodynamics, write down a relation between $Q, p_{\mathrm{a}}, V, V_0$ and $k$.

Solution:
2251 Upvotes
Verified Answer
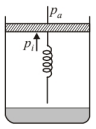
It is considered that piston is mass less and piston is balanced by atmospherioc pressure $\left(p_{\mathrm{a}}\right)$, so the initial pressure of system inside the cylinder $\left(p_i\right)$.
(a) At initial position when system in equilibrium hence, $p_i=p_a$
(b) On supplying heat volume of the gas expands from $V_0$ to $V_1$ and spring stretched also.
So increase in volume of the gas $=V_1-V_0$ If displacement of piston is $x$ then volume increase in $V$ (cylinder).
Hence, extension in the spring is :
Let $\mathrm{Area}=A$
$$
x=\frac{V_1-V_0}{\text { Area }}=\left(\frac{V_1-V_0}{A}\right)
$$
Force exerted by the spring on the piston
$$
F_s=k x=\frac{k\left(V_1-V_0\right)}{A}
$$
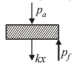
As the piston is of unit area of cross section so $(A=1)$. Hence, final total pressure on gas,
$$
\begin{aligned}
p_f &=p_a+k x \\
&=p_a+k \times\left(V_1-V_0\right)
\end{aligned}
$$
(c) By first law of thermodynamics
$$
d Q=d U+d W
$$
If $T$ is final temperature of the gas, then increase in internal energy
$$
d U=C_V\left(T-T_0\right)=C_V\left(T-T_0\right),
$$
where $T_0=$ initial temperature of gas
We can write,
$$
T_f=T=\frac{p_1 V_1}{R}=\left[p_a+k\left(V_1-V_0\right)\right] \frac{V_1}{R}
$$
Work done by the gas
$=p d V+$ increase in PE of the spring
$$
d W=p_a\left(V_1-V_0\right)+\frac{1}{2} k x^2
$$
So, we can written as
$$
\begin{aligned}
d Q &=d U+d W \\
&=C_V\left(T-T_0\right)+p_a\left(V-V_0\right)+\frac{1}{2} k x^2 \\
d Q &=C_V\left(T-T_0\right)+p_a\left(V-V_0\right)+\frac{1}{2} k\left(V_1-V_0\right)^2
\end{aligned}
$$
It is the required relation.
(a) At initial position when system in equilibrium hence, $p_i=p_a$
(b) On supplying heat volume of the gas expands from $V_0$ to $V_1$ and spring stretched also.
So increase in volume of the gas $=V_1-V_0$ If displacement of piston is $x$ then volume increase in $V$ (cylinder).
Hence, extension in the spring is :
Let $\mathrm{Area}=A$

$$
x=\frac{V_1-V_0}{\text { Area }}=\left(\frac{V_1-V_0}{A}\right)
$$
Force exerted by the spring on the piston
$$
F_s=k x=\frac{k\left(V_1-V_0\right)}{A}
$$
As the piston is of unit area of cross section so $(A=1)$. Hence, final total pressure on gas,
$$
\begin{aligned}
p_f &=p_a+k x \\
&=p_a+k \times\left(V_1-V_0\right)
\end{aligned}
$$

(c) By first law of thermodynamics
$$
d Q=d U+d W
$$
If $T$ is final temperature of the gas, then increase in internal energy
$$
d U=C_V\left(T-T_0\right)=C_V\left(T-T_0\right),
$$
where $T_0=$ initial temperature of gas
We can write,
$$
T_f=T=\frac{p_1 V_1}{R}=\left[p_a+k\left(V_1-V_0\right)\right] \frac{V_1}{R}
$$
Work done by the gas
$=p d V+$ increase in PE of the spring
$$
d W=p_a\left(V_1-V_0\right)+\frac{1}{2} k x^2
$$
So, we can written as
$$
\begin{aligned}
d Q &=d U+d W \\
&=C_V\left(T-T_0\right)+p_a\left(V-V_0\right)+\frac{1}{2} k x^2 \\
d Q &=C_V\left(T-T_0\right)+p_a\left(V-V_0\right)+\frac{1}{2} k\left(V_1-V_0\right)^2
\end{aligned}
$$
It is the required relation.
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.