Search any question & find its solution
Question:
Answered & Verified by Expert
Consider the circuit arrangement shown in figure for studying input and output characteristics of $\mathrm{n}-\mathrm{p}-\mathrm{n}$ trasnsistor in CE configuration.
Select the values of $R_B$ and $R_C$ for a transistor whose $V_{B E}=$ $0.7 \mathrm{~V}$, so that the transistor is operating at point $\mathrm{Q}$ as shown in the characteristics (see figure).
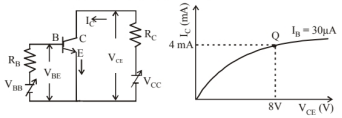
Given that the input impedance of the transistor is very small and $\mathrm{V}_{\mathrm{CC}}=\mathrm{V}_{\mathrm{BB}}=16 \mathrm{~V}$, also find the voltage gain and power gain of circuit making appropriate assumptions.
Select the values of $R_B$ and $R_C$ for a transistor whose $V_{B E}=$ $0.7 \mathrm{~V}$, so that the transistor is operating at point $\mathrm{Q}$ as shown in the characteristics (see figure).

Given that the input impedance of the transistor is very small and $\mathrm{V}_{\mathrm{CC}}=\mathrm{V}_{\mathrm{BB}}=16 \mathrm{~V}$, also find the voltage gain and power gain of circuit making appropriate assumptions.
Solution:
1408 Upvotes
Verified Answer
As given that,
$$
\begin{aligned}
&\mathrm{V}_{\mathrm{BE}}=0.7 \mathrm{~V}, \mathrm{~V}_{\mathrm{CC}}=\mathrm{V}_{\mathrm{BB}}=16 \mathrm{~V} \\
&\mathrm{~V}_{\mathrm{CE}}=8 \mathrm{~V} \quad \text { (from graph) } \\
&\mathrm{I}_{\mathrm{C}}=4 \mathrm{~mA}=4 \times 10^{-3} \mathrm{~A} \\
&\mathrm{I}_{\mathrm{B}}=30 \mu \mathrm{A}=30 \times 10^{-6} \mathrm{~A}
\end{aligned}
$$
For ouput characteristic at Point Q, Applying Kirchhoff's law in collector emitterloop.
$$
\begin{aligned}
&\mathrm{V}_{\mathrm{CC}}=\mathrm{I}_{\mathrm{C}} \mathrm{R}_{\mathrm{C}}+\mathrm{V}_{\mathrm{CE}} \\
&\quad \mathrm{R}_{\mathrm{C}}=\frac{\mathrm{V}_{\mathrm{CC}}-\mathrm{V}_{\mathrm{CE}}}{\mathrm{I}_{\mathrm{C}}}=\frac{16-8}{4 \times 10^{-3}}=\frac{8 \times 1000}{4}=2 \mathrm{k} \Omega \\
&\mathrm{R}_{\mathrm{C}}=2 \mathrm{k} \Omega
\end{aligned}
$$
Now applying Kirchhoff's law in base-emitter loop
$$
\begin{aligned}
& V_{B B}=I_B R_B+V_{B E} \\
R_B &=\frac{V_{B B}-V_{B E}}{I_B}=\frac{16-0.7}{30 \times 10^{-6}}=\frac{15.3 \times 10^6}{30} \\
&=510 \times 10^3 \Omega=510 \mathrm{k} \Omega
\end{aligned}
$$
For voltage gain $=A v=+\beta \frac{R_C}{R_B}$
$$
\beta=\frac{\mathrm{I}_{\mathrm{C}}}{\mathrm{I}_{\mathrm{B}}}=\frac{4 \times 10^{-3}}{30 \times 10^{-6}}=133
$$
For Average voltage gain
$$
=\beta \frac{\mathrm{R}_{\mathrm{C}}}{\mathrm{R}_{\mathrm{B}}}=\frac{133 \times 2 \times 10^3}{510 \times 10^3}=0.52
$$
Power gain $=\beta \times$ Voltage gain
$$
=133 \times 0.52=69.33
$$
$$
\begin{aligned}
&\mathrm{V}_{\mathrm{BE}}=0.7 \mathrm{~V}, \mathrm{~V}_{\mathrm{CC}}=\mathrm{V}_{\mathrm{BB}}=16 \mathrm{~V} \\
&\mathrm{~V}_{\mathrm{CE}}=8 \mathrm{~V} \quad \text { (from graph) } \\
&\mathrm{I}_{\mathrm{C}}=4 \mathrm{~mA}=4 \times 10^{-3} \mathrm{~A} \\
&\mathrm{I}_{\mathrm{B}}=30 \mu \mathrm{A}=30 \times 10^{-6} \mathrm{~A}
\end{aligned}
$$
For ouput characteristic at Point Q, Applying Kirchhoff's law in collector emitterloop.
$$
\begin{aligned}
&\mathrm{V}_{\mathrm{CC}}=\mathrm{I}_{\mathrm{C}} \mathrm{R}_{\mathrm{C}}+\mathrm{V}_{\mathrm{CE}} \\
&\quad \mathrm{R}_{\mathrm{C}}=\frac{\mathrm{V}_{\mathrm{CC}}-\mathrm{V}_{\mathrm{CE}}}{\mathrm{I}_{\mathrm{C}}}=\frac{16-8}{4 \times 10^{-3}}=\frac{8 \times 1000}{4}=2 \mathrm{k} \Omega \\
&\mathrm{R}_{\mathrm{C}}=2 \mathrm{k} \Omega
\end{aligned}
$$
Now applying Kirchhoff's law in base-emitter loop
$$
\begin{aligned}
& V_{B B}=I_B R_B+V_{B E} \\
R_B &=\frac{V_{B B}-V_{B E}}{I_B}=\frac{16-0.7}{30 \times 10^{-6}}=\frac{15.3 \times 10^6}{30} \\
&=510 \times 10^3 \Omega=510 \mathrm{k} \Omega
\end{aligned}
$$
For voltage gain $=A v=+\beta \frac{R_C}{R_B}$
$$
\beta=\frac{\mathrm{I}_{\mathrm{C}}}{\mathrm{I}_{\mathrm{B}}}=\frac{4 \times 10^{-3}}{30 \times 10^{-6}}=133
$$
For Average voltage gain
$$
=\beta \frac{\mathrm{R}_{\mathrm{C}}}{\mathrm{R}_{\mathrm{B}}}=\frac{133 \times 2 \times 10^3}{510 \times 10^3}=0.52
$$
Power gain $=\beta \times$ Voltage gain
$$
=133 \times 0.52=69.33
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.